数据结构作业题：列车调度 —— 最长递增子序列

列车调度

火车站的列车调度铁轨的结构如下图所示。

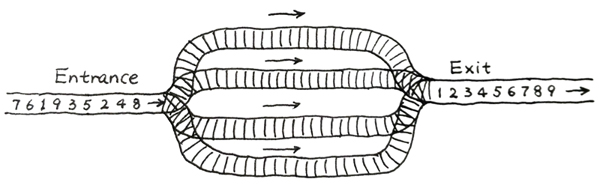
两端分别是一条入口（Entrance）轨道和一条出口（Exit）轨道，它们之间有N条平行的轨道。每趟列车从入口可以选择任意一条轨道进入，最后从出口离开。在图中有9趟列车，在入口处按照{8，4，2，5，3，9，1，6，7}的顺序排队等待进入。如果要求它们必须按序号递减的顺序从出口离开，则至少需要多少条平行铁轨用于调度？

输入格式：

输入第一行给出一个整数N (2 ≤ N ≤105)，下一行给出从1到N的整数序号的一个重排列。数字间以空格分隔。

输出格式：

在一行中输出可以将输入的列车按序号递减的顺序调离所需要的最少的铁轨条数。

输入样例：

9
8 4 2 5 3 9 1 6 7

输出样例：

4

这个问题是一个经典的 列车调度问题，可以用 最长递增子序列 (LIS) 的思路来解，但这里需要的是 最少轨道数，其实等价于求 序列的最长递减子序列的长度，不过更准确地说，是最少下降子序列划分个数，等价于求 最长上升子序列的长度（Dilworth 定理）。

问题分析

我们有编号 1 到 N 的一个排列，要求按 从大到小 的顺序离开出口。

入口顺序：例如 8 4 2 5 3 9 1 6 7

出口顺序要求：9 8 7 6 5 4 3 2 1（递减）

在平行轨道上，列车可以任意进入，但一旦进入某轨道，就必须在该轨道上保持 从入口到出口方向 的顺序，并且每条轨道上列车编号必须 递增（因为出口方向是递减，所以轨道内部必须递增才能保证出去时大的先出）。

转化

假设轨道内部列车编号是递增的，那么最后离开时，从一条轨道上出去的顺序是 栈 的性质（后进先出），所以每条轨道可以看作一个栈，栈顶元素是当前轨道上编号最大的车。

当我们处理一辆新车时，我们要把它放到某个轨道的栈顶，且必须满足该轨道的栈顶元素比新车编号小（因为轨道内要递增）。

为了用最少的轨道，我们每次选择 栈顶元素大于新车编号且最接近新车编号 的轨道，放进去（这样可以让轨道利用率高）。如果所有栈顶元素都比新车小，就新开一个轨道。

算法

维护一个数组 top[]，top[i] 表示第 i 条轨道的栈顶元素（当前轨道上编号最大的车）。

遍历输入序列的每个数 x：

• 在 top 数组中找 第一个大于等于 x 的数，用 x 替换它（相当于把 x 压入该轨道）。
• 如果找不到，就在 top 末尾添加 x（新开一条轨道）。

因为 top 数组是 单调递增 的，所以可以用二分查找。

最后 top 数组的长度就是最少需要的轨道数。

为什么等价于最长上升子序列长度？

Dilworth 定理：一个序列的最少下降子序列划分个数 = 最长上升子序列长度。

这里我们要求的是最少轨道数，每条轨道是一个上升子序列（因为轨道内编号递增），所以最少轨道数 = 最长下降子序列长度。

但更简单的是直接模拟上述贪心 + 二分过程。

示例

输入：

9
8 4 2 5 3 9 1 6 7

模拟过程（top 数组记录每条轨道栈顶元素）：

1. 8 → top = [8]
2. 4 → 找第一个 ≥4 的是 8，替换 → top = [4]
3. 2 → 找第一个 ≥2 的是 4，替换 → top = [2]
4. 5 → 找不到 ≥5 的，新增 → top = [2, 5]
5. 3 → 找第一个 ≥3 的是 5，替换 → top = [2, 3]
6. 9 → 找不到 ≥9 的，新增 → top = [2, 3, 9]
7. 1 → 找第一个 ≥1 的是 2，替换 → top = [1, 3, 9]
8. 6 → 找第一个 ≥6 的是 9，替换 → top = [1, 3, 6]
9. 7 → 找第一个 ≥7 的是 无（6<7, 3<7, 1<7），新增 → top = [1, 3, 6, 7]

最终轨道数 = 4。

代码实现

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
    int N;
    cin >> N;
    vector<int> top; // 每条轨道的栈顶元素，保持递增
    
    for (int i = 0; i < N; i++) {
        int x;
        cin >> x;
        // 二分查找第一个大于等于 x 的位置
        auto it = lower_bound(top.begin(), top.end(), x);
        if (it == top.end()) {
            // 所有栈顶都小于 x，新开轨道
            top.push_back(x);
        } else {
            // 替换该栈顶
            *it = x;
        }
    }
    
    cout << top.size() << endl;
    
    return 0;
}