《最优化理论与方法》复习笔记
最优化理论与方法
《最优化原理与应用》期末复习重点总览
第一部分:课程知识体系与核心思想
- 核心理念:本课程内容(凸优化、迭代算法等)是机器学习、深度学习模型的底层数学基础。理解这些知识,有助于你从原理上把握模型(如交叉熵损失函数)为何有效,以及如何求解,这是区别于单纯使用工具的“职业培训”的关键。
第二部分:各章节重点梳理及题型预测
第一讲:最优化问题分类
重点概念:
- 约束优化 vs. 无约束优化
- 线性规划、二次规划
- 要求:清晰掌握定义和分类。
第二讲:凸集合
- 定义:集合中任意两点的连线仍在该集合内。(几何直观:没有“凹陷”)
证明方法:
- 直接用定义证明。
- 利用凸集合的运算性质(如:两个凸集的交集、仿射变换后的集仍是凸集)。
题型预测:
- 填空/简答:凸集定义。
- 证明题:证明某个集合(如线性不等式约束构成的可行域)是凸集。
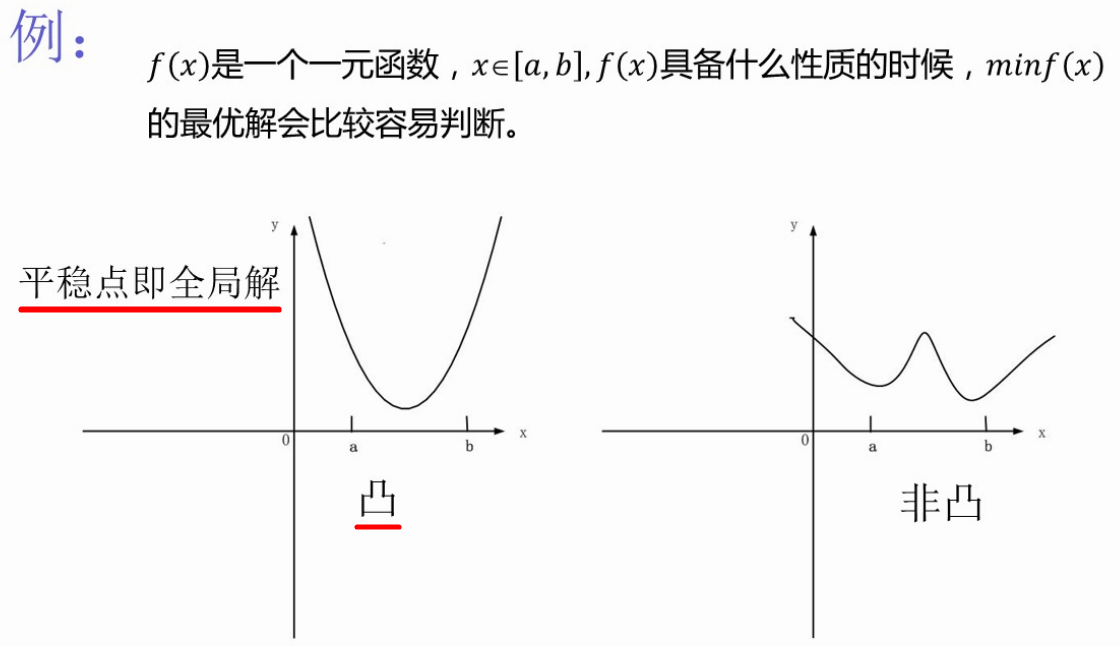
第三讲:凸函数
- 定义:函数图形上任意两点的连线位于函数图像之上。
证明方法:
- 利用定义。
- 利用Hessian矩阵半正定/正定(对于二阶可微函数)。
题型预测:
- 简答/证明:凸函数定义或证明给定函数(如二次函数)是凸函数。
- 理解:能画出凸/非凸函数的直观图形。
第四讲:凸优化问题
- 定义:在凸集上最小化凸函数的问题。
核心性质(非常重要!):
- 对于无约束凸优化:梯度为零的点就是全局最优解。
- 对于约束凸优化:局部最优解就是全局最优解。
- (此性质是很多机器学习损失函数求导求解的理论依据)。
题型预测:
- 简答/论述:什么是凸优化问题?它有什么优良性质?为什么这些性质在机器学习中很重要?(可能结合交叉熵损失例子)。
第五讲:无约束优化方法
四大迭代下降算法(必考!):
- 坐标轴交替下降法
- 梯度下降法
- 牛顿法
- 共轭梯度法
- 共同点:都是迭代下降算法(从一个初始点,找下降方向,确定步长,循环迭代)。
各算法特点对比(可能出填空、选择或简答):
- 最“廉价”的方法:坐标轴交替下降法(无需计算梯度,沿坐标轴方向搜索)。
- 计算量最大的方法:牛顿法(需要计算二阶Hessian矩阵及其逆)。
- 共轭梯度法的思想:通过变换,将问题转化为在新的一组“共轭方向”上做坐标下降。
题型预测:
- 填空题:“请写出三种无约束优化方法:、、___”(注意别漏掉“坐标轴交替下降法”)。
- 简答题:比较几种算法的优缺点或共同点。
- 计算题(高频):梯度下降法的计算步骤(给定函数,求梯度,迭代一步或两步)。
第六讲:对偶理论与KKT条件
KKT条件:约束优化问题最优解的必要条件(对于凸优化也是充分的)。
- 要求:掌握课本上的例题,会计算。
拉格朗日对偶问题:
构造步骤(三步,缺一不可,有步骤分!):
- 写出拉格朗日函数。
- 拉格朗日对偶函数。
- 形成拉格朗日对偶问题。
- 目的:原问题难求解时,对偶问题可能更简单。
题型预测:
- 计算/证明题:写出给定优化问题的KKT条件或对偶问题。
- 简答题:为什么要研究对偶理论?
第七讲:实验与实践
- 工具:学会使用
CVXPY等凸优化求解工具。 - 实验检查:最后一次实验课会进行检查,请务必完成。
- 理念:不仅要懂理论,也要会建模和求解。
第三部分:应试技巧与注意事项
答题策略:
- 合理分配时间,先通览全卷。
- 概念题不要写得过于冗长,抓核心要点。
- 给计算题留出充足时间(如梯度下降计算量较大)。
得分要点:
- 写对偶问题时,必须写出完整的三个步骤,跳步会扣分。
- 对于定义、性质等概念,表述要严谨准确。
复习建议:
- 以课件和课本例题为基础,巩固基本概念和算法步骤。
- 重新温习习题和实验内容,特别是梯度下降、KKT条件和对偶问题的例题。
总结:本次考试重点非常明确,核心围绕 “凸性”(凸集、凸函数、凸优化)、“四大无约束算法” 以及 “对偶理论与KKT条件” 展开。复习时请将理论与机器学习模型的联系(如凸函数性质如何保证全局最优)结合起来理解,这不仅是考试重点,更是课程的精髓所在。
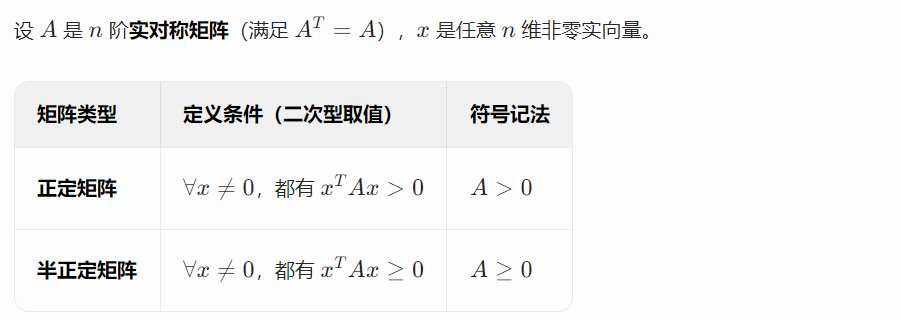
(一)基本概念
1、第1讲 导入
(1、)最优化问题基本概念
什么是最优化问题

基本形式

分类

(2、)前置知识
向量加减法
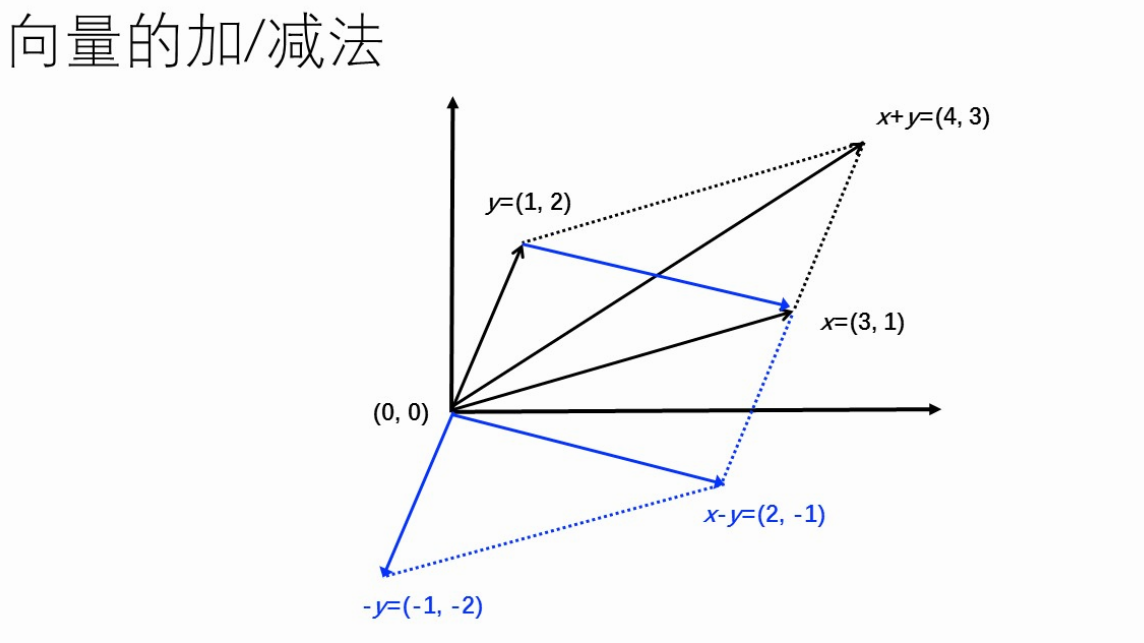
梯度、Hesse矩阵

梯度计算:

黑塞矩阵计算:
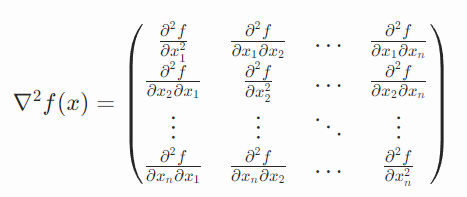
内积


+【习题★】求梯度、Hesse矩阵大题,结合线性代数

【习题】简单求梯度

▽f(x)=2x1 + 2x2
▽f((2,1)T)=4+2=6
2、第2讲 凸集
凸集的定义
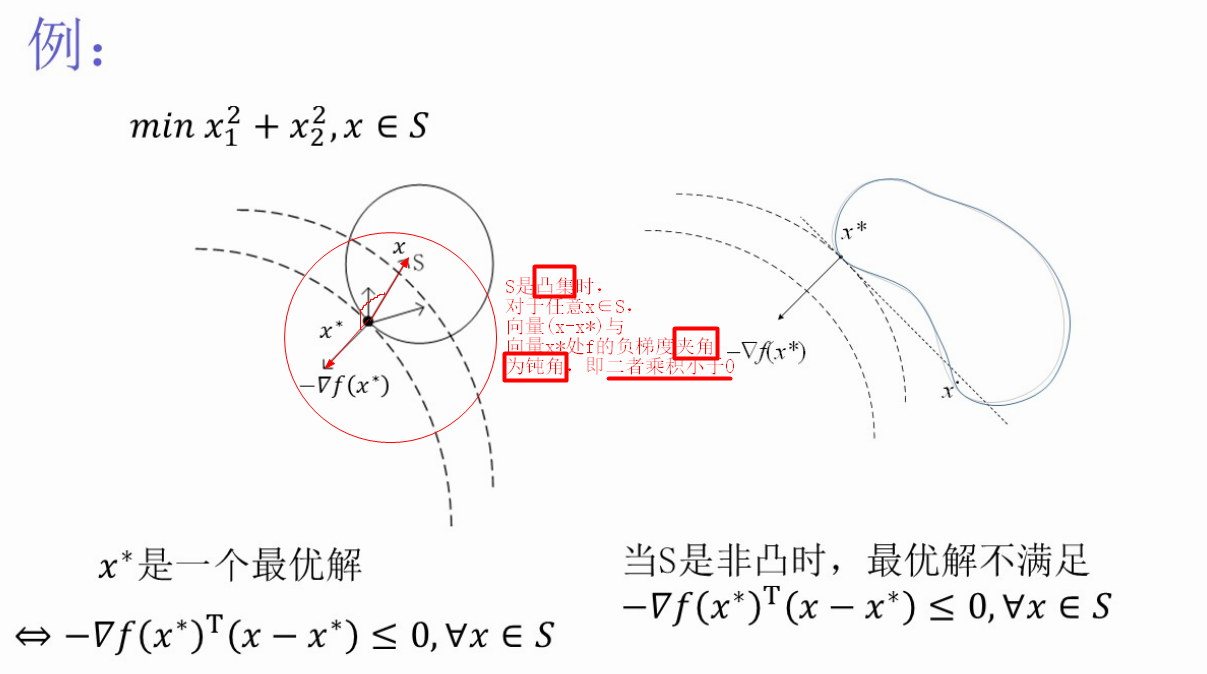
观察:S是凸集时,对任意x∈S,使(x-x*)与x*处负梯度夹角大于90度
定义★★:
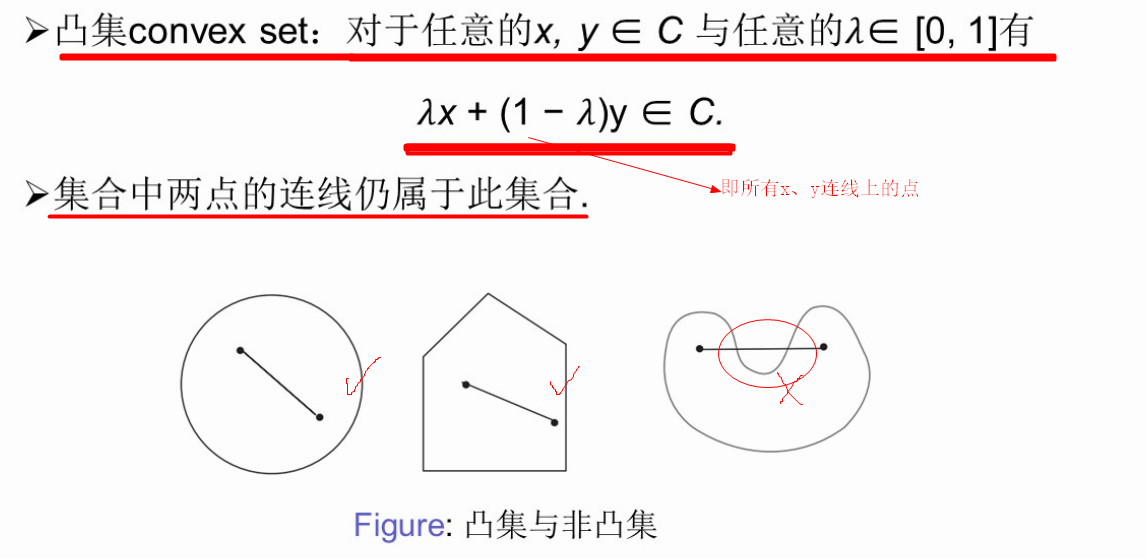
【例题】写出三角形C是凸集的条件
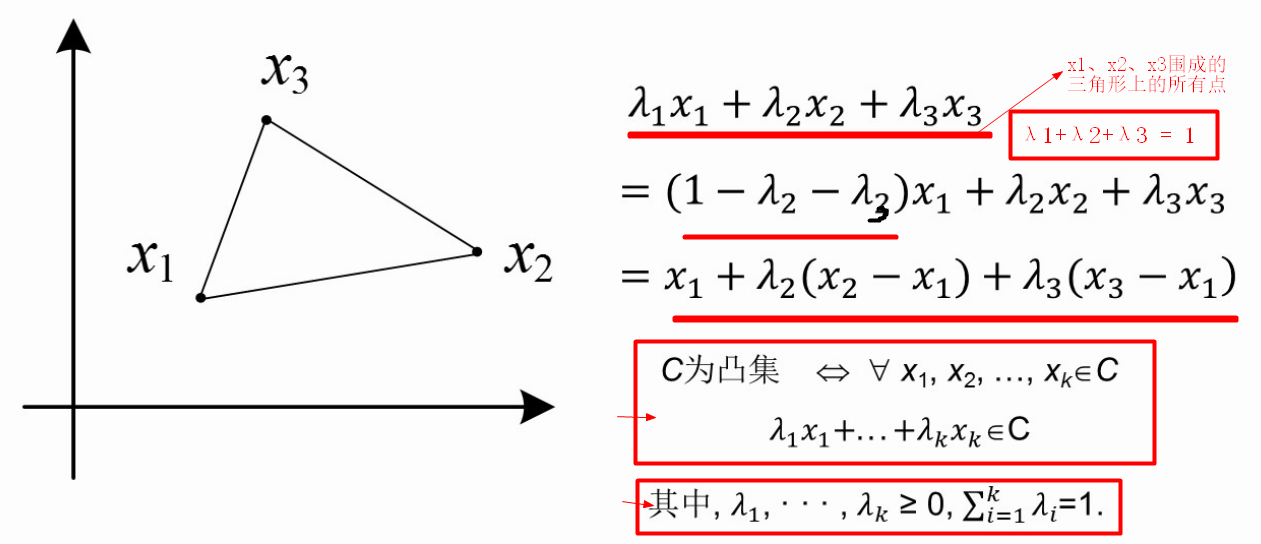

常见的凸集:超平面、半空间、多面体、欧氏球、二阶锥


由线性等式刻画的集合是多面体。线性等式刻画的集合属于多面体,因为线性等式可以等价转化为两个半空间的交集,而多面体的定义是 “有限个半空间的交集”。


||·||2是向量长度。★

+【例题】判断S是凸集合吗


凸集与凸集的交集还是凸集。
凸集与凸集的并集还是凸集。



凸集的性质


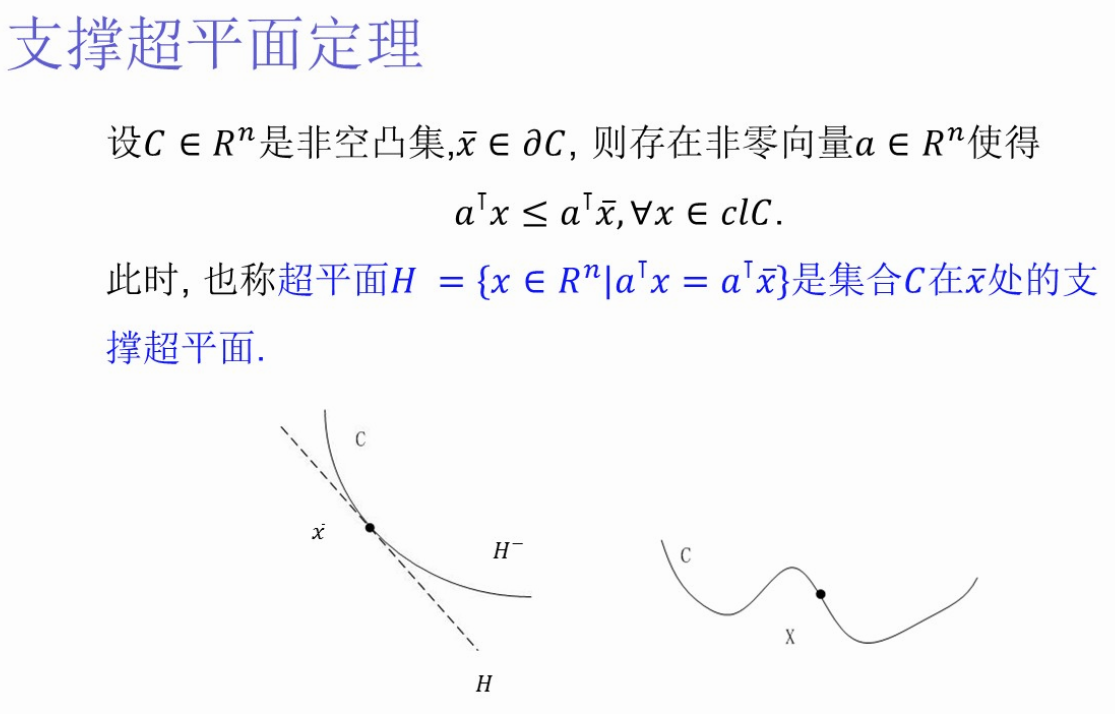
相当于凸集边上一点的一个切线(切面)
3、第3讲 凸函数:定义与基本性质
(1、)定义★★★★
f(ax+(1-a)y) <= af(x)+(1-a)f(y)
严格凸函数?
凹函数?

(2、)常见的凸函数★★★
线性函数、二次函数、最小二乘函数、p范数

(3、)凸函数的性质★★★(3点)

1.凸函数一定是连续函数
2.f(x)是凸函数<=>f(x+ay)是凸函数
3.f(x)是在C上的凸函数的充要条件是__________。
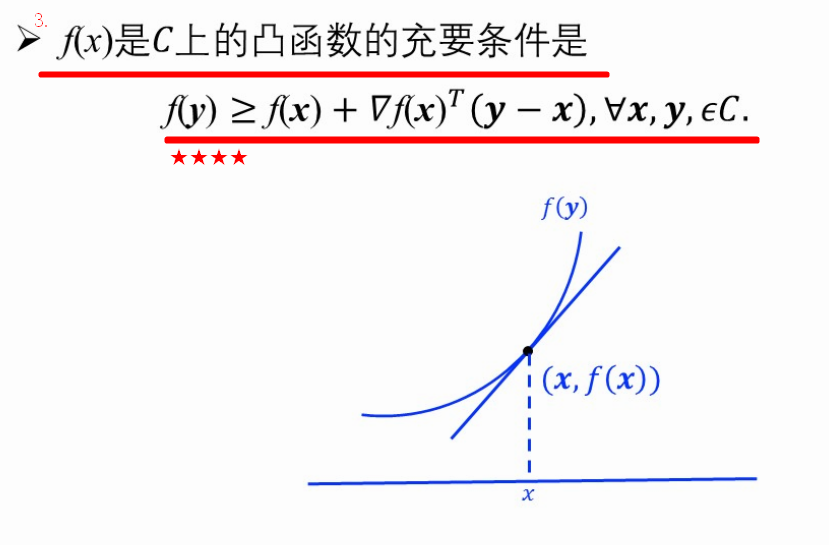
【习题】易错★★写出过函数一点的直线
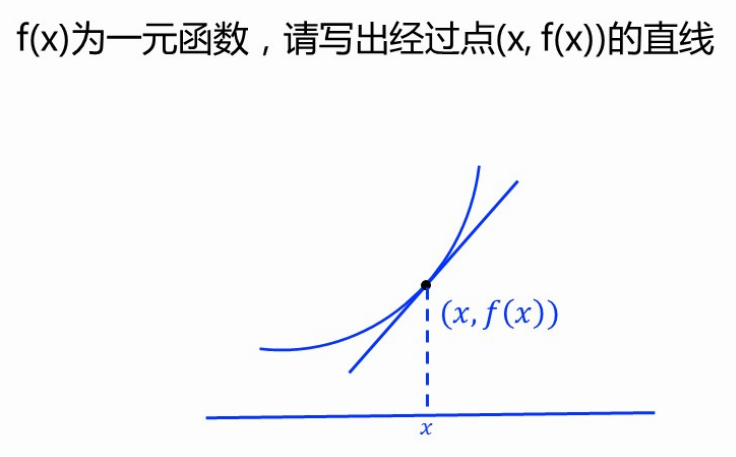

点(x,f(x)),则符号x被使用了,故自变量采用t
y - f(x) = ∇f(x)T(t-x)
y = ∇f(x)T(t-x) + f(x)
+【证明题】★★★★证明凸函数性质3:f(y)>=f(x)+∇f(x)T(y-x)


+【习题】★★★写出泰勒公式

+【证明题】f(x)二阶连续可微,是凸函数<=>f(x)Hesse矩阵>=0(半正定)





(4、)保持函数凸性的运算有哪些?
透视函数、非负组合、一组凸函数求最大
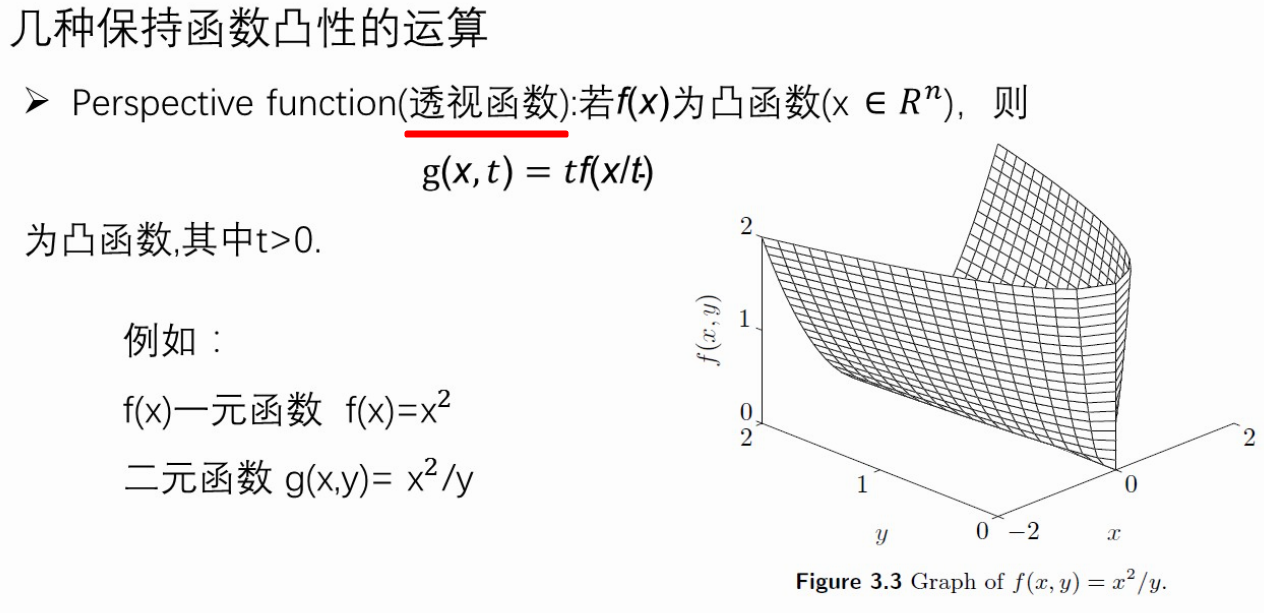
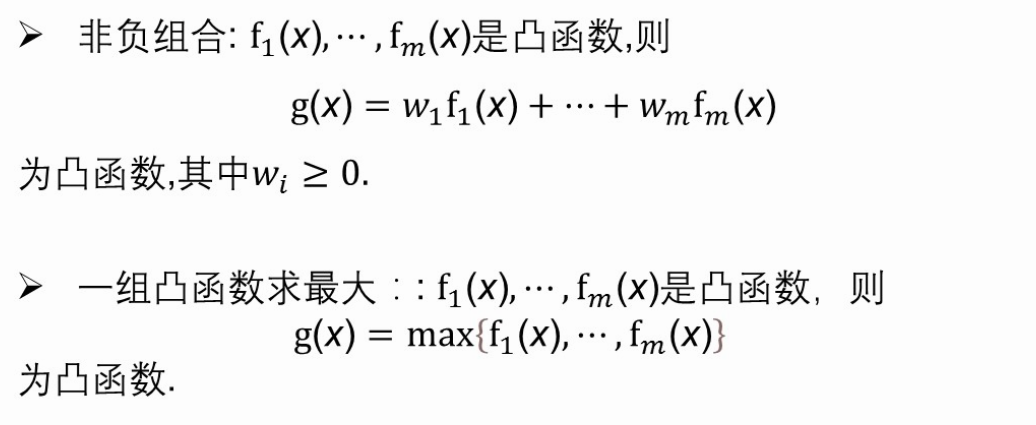
(5、)凸集与凸函数的关联
凸函数的水平集必为凸集,但水平集均为凸集的函数不一定是凸函数。

+【习题】★★★证明凸函数组合是凸函数


总结

4、第4讲 凸优化问题


【习题】★求最优解和最优值


【例题】★判断问题是不是凸优化问题


【线性代数】判断矩阵是否正定


(1、)区分凸优化与非凸优化
对于凸优化问题,局部最优解即全局最优解。

(2、)凸优化问题的最优性条件
x*是最优解 <=> ∇f(x*)T(x-x*)>=0 <=> f(x) >= f(x*) +∇f(x*)T(x-x*) >= f(x*)

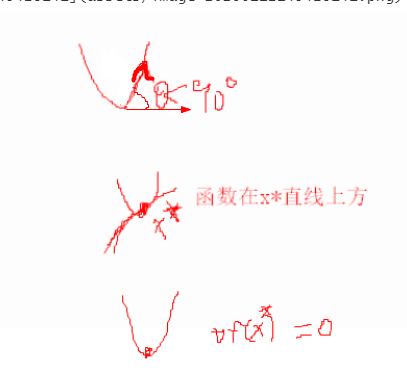
∇f(x*) = 0

(3、)常见凸优化问题
线性规划、二阶锥规划、几何规划

(4、)线性规划




(5、)凸二次规划

(6、)带二次约束的二次规划

(7、)二阶锥规划

(8、)集合的中心问题



(二)无约束优化问题
1、第5讲 最优性条件及线搜索方法
(1、)最优性条件
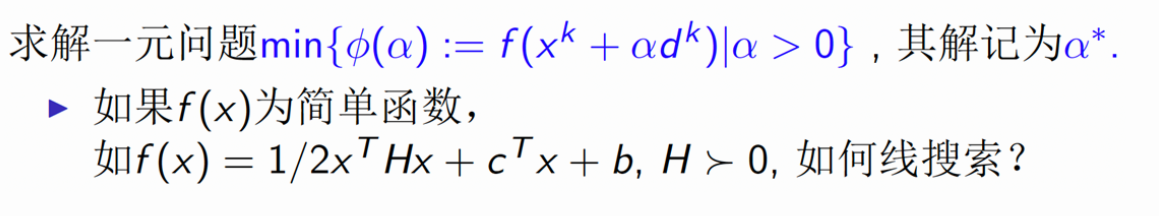

严格最优解:梯度=0,Hesse矩阵正定
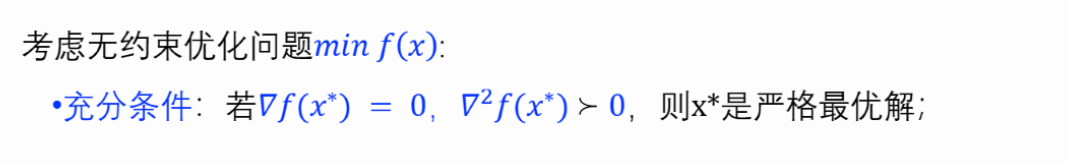
【习题】求梯度


【习题】选择合适的梯度下降方向


(2、)基于线搜索的下降算法基本思路【描述★★★】

x_0 k=0
while (true) {
if (满足终止条件) return; // 终止条件:梯度低于阈值 || 下降距离低于阈值
寻找下降方向d_k // 梯度下降法
选择合适步长a_k,使f(x_k+a_k*d_k<f(x_k))
令x_k+1 = x_k + a_k*d_k; k = k+1
}
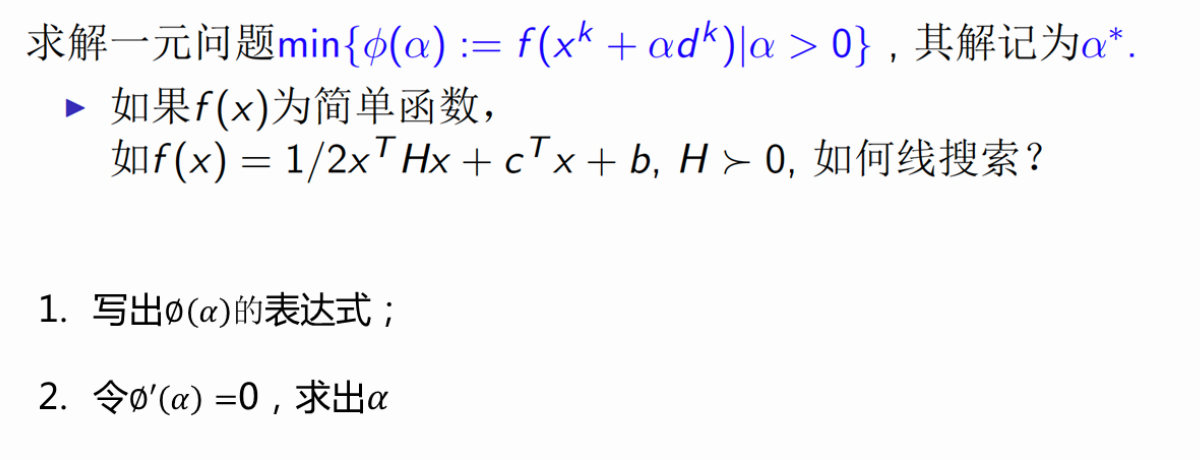
基于搜索区间的直接搜索法
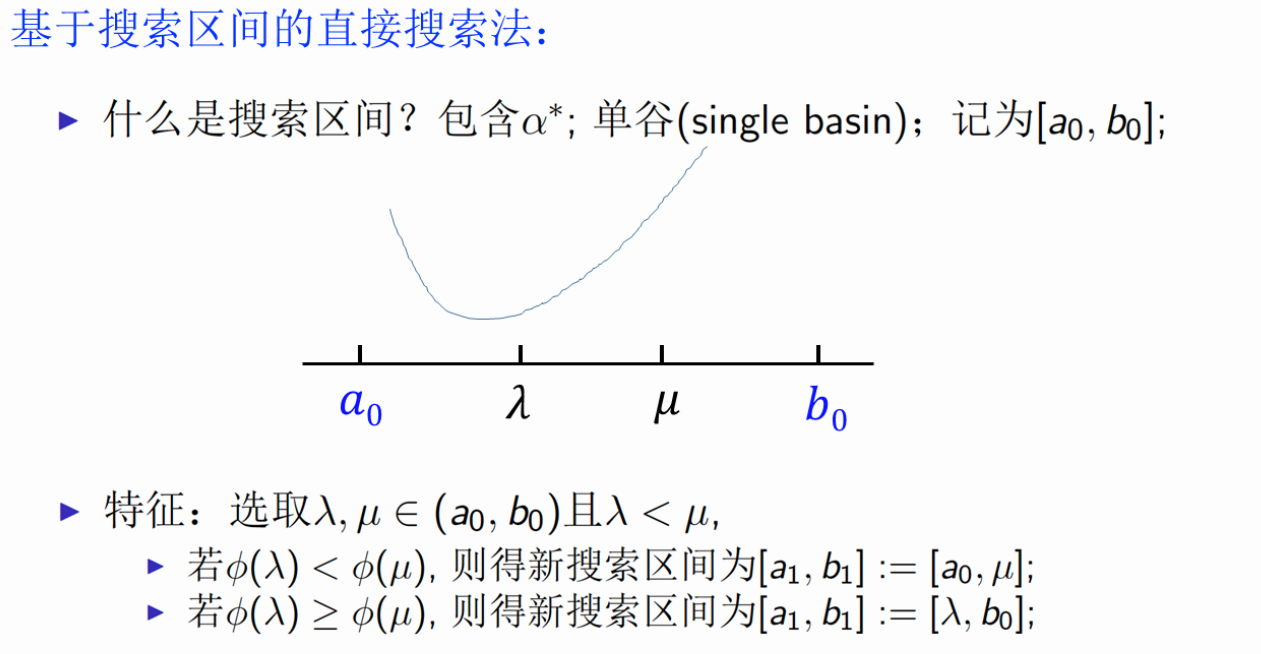
直接搜索法--均匀搜索法、黄金区间法


【习题】证明黄金区间法


2、第6讲 无约束优化问题常用求解方法
线搜索下降算法

(1、)坐标轴交替下降法

【描述思路:给定初始值x_0,沿着坐标轴e_1...e_n进行搜索、
优点:不需要成本即可获得搜索方向、
缺点:可能无法收敛】

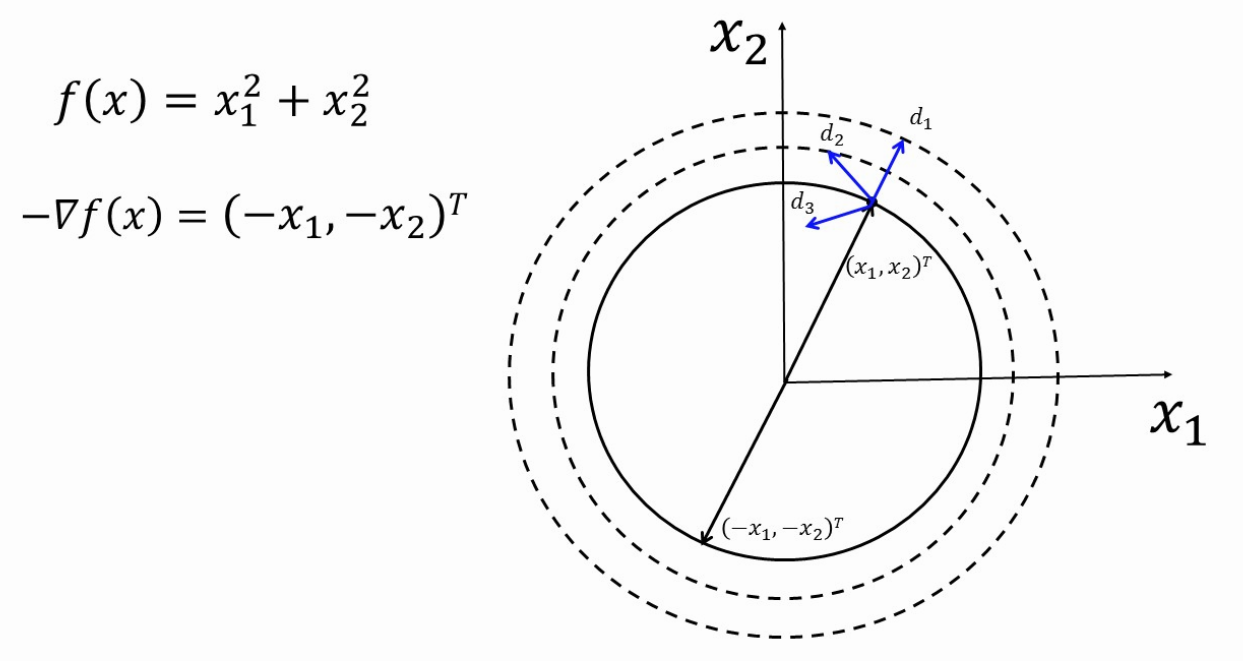
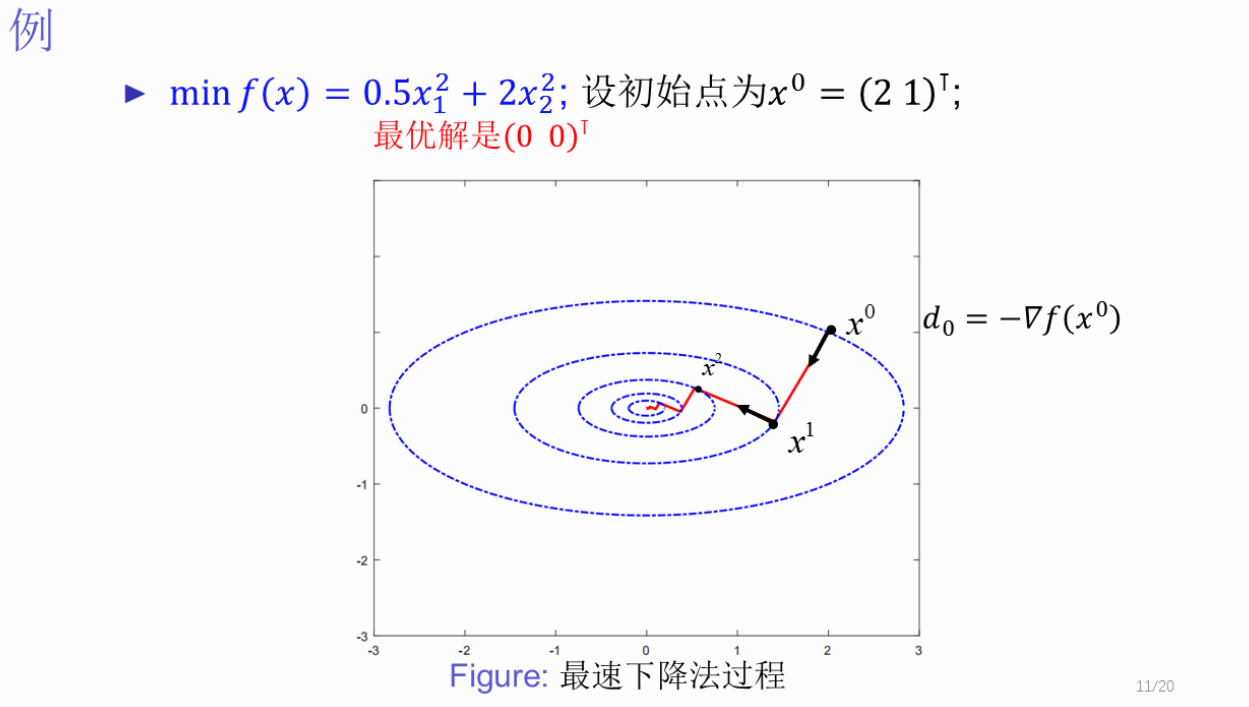
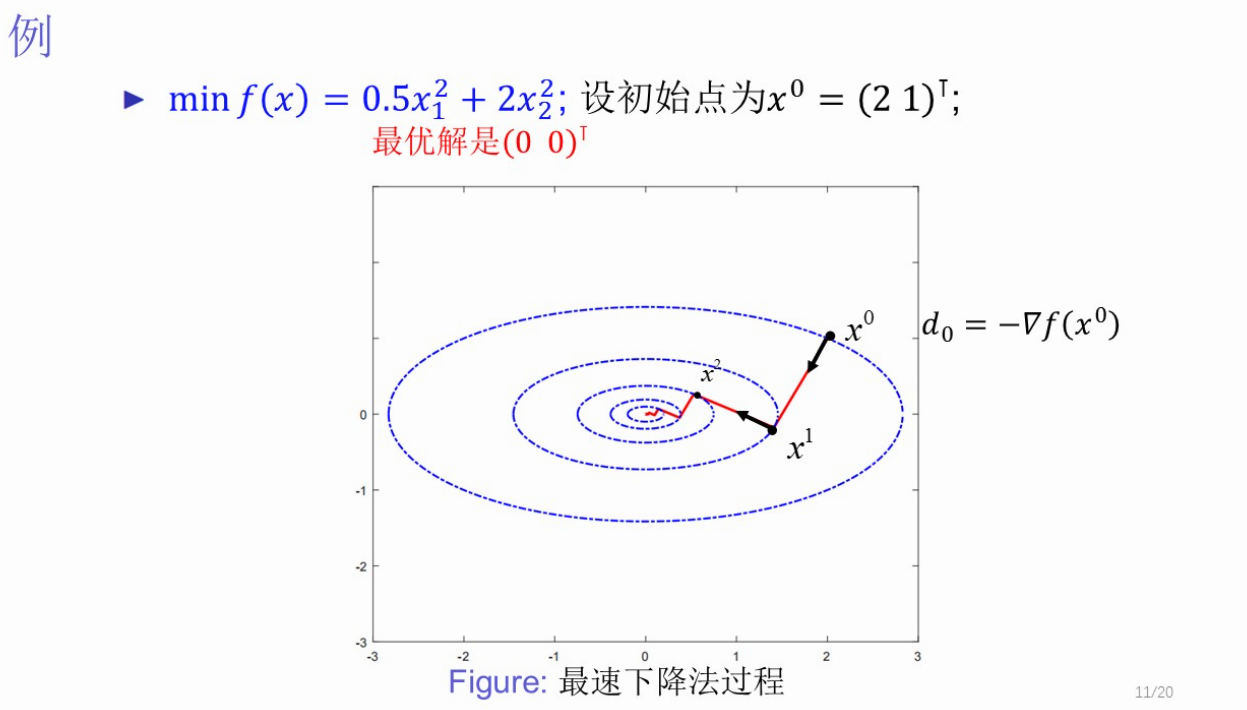
(2、)最速下降法(梯度下降法)
【描述基本思想:选择x_k处的负梯度为搜索方向,即d_k=-∇f(x_k)
优点:简单直观;收敛;搜索方向只需计算梯度
缺点:收敛速度慢、Zigzag现象、不具备二次终止性(并不能在有限步内得到最优解)】



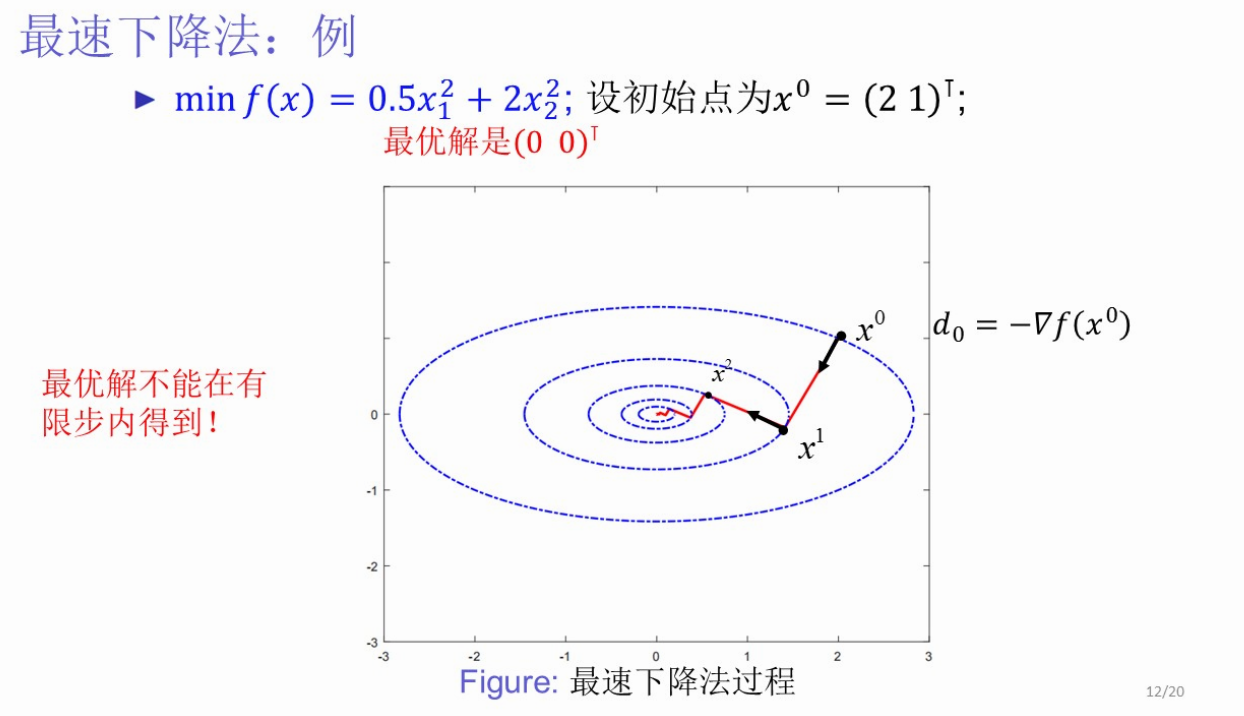
(3、)牛顿法
+【习题】导入-求函数最小值
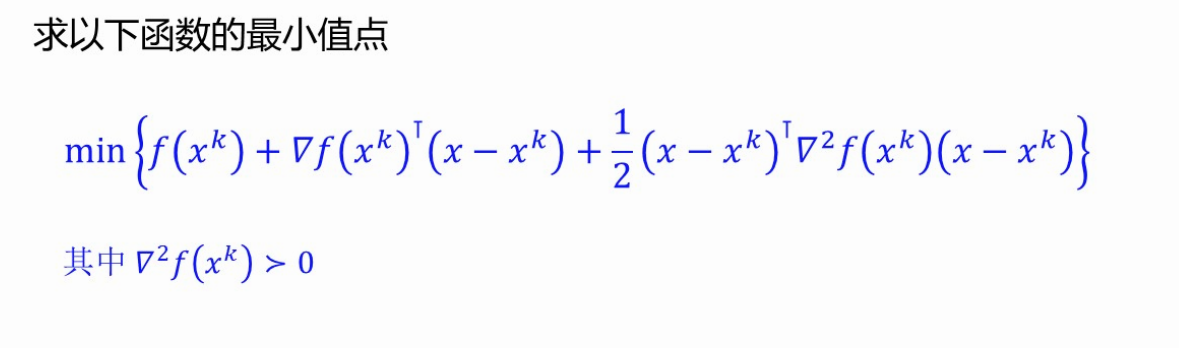

+【习题】导入-写出泰勒展开式



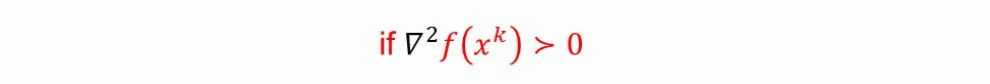
【描述基本思路、
优点:x_0接近x*且Hesse矩阵满足较好性质时二阶收敛;满足二次终止性、
缺点:计算量大、使用范围窄】


+【习题★★★】利用牛顿法求函数最小值

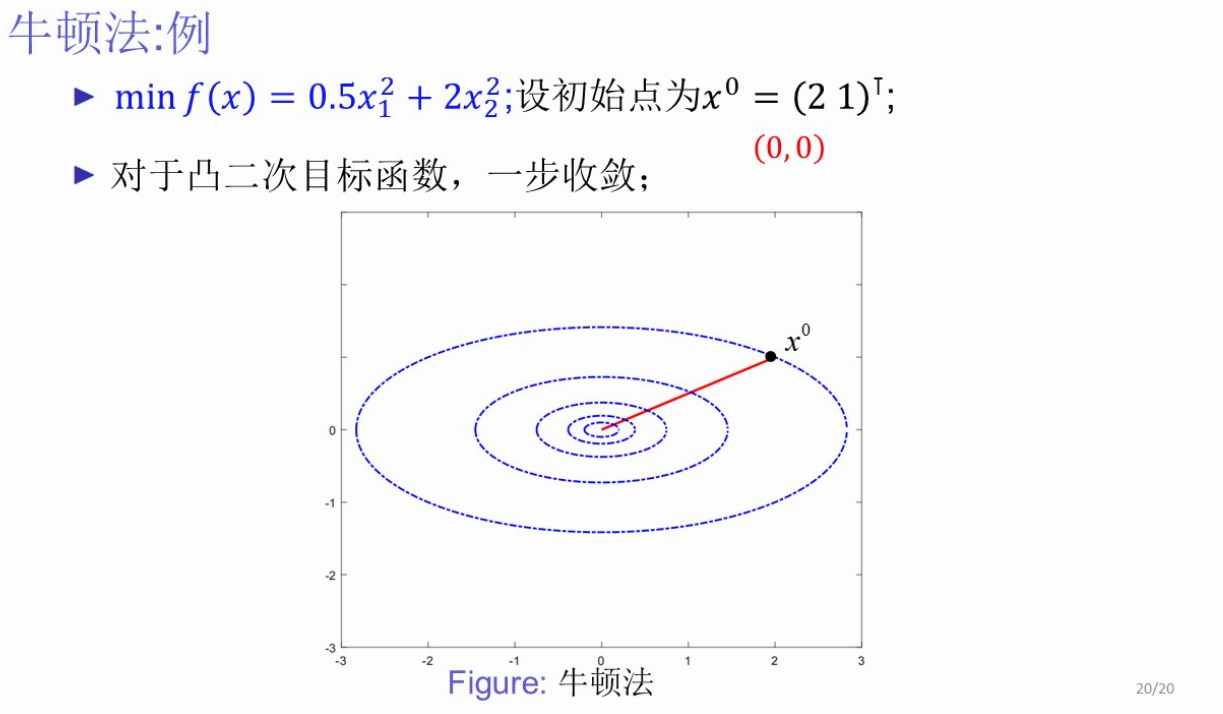
修正牛顿法★★★
【描述:两个修正,1.对步长的修正:如果a_k=1不能让目标函数充分下降就采用线搜索重新确定a_k,2.对方向(Hesse矩阵)的修正,如果不正定,B_k+=λI,保证B_k正定】


3、+第7讲 (4、)共轭梯度法
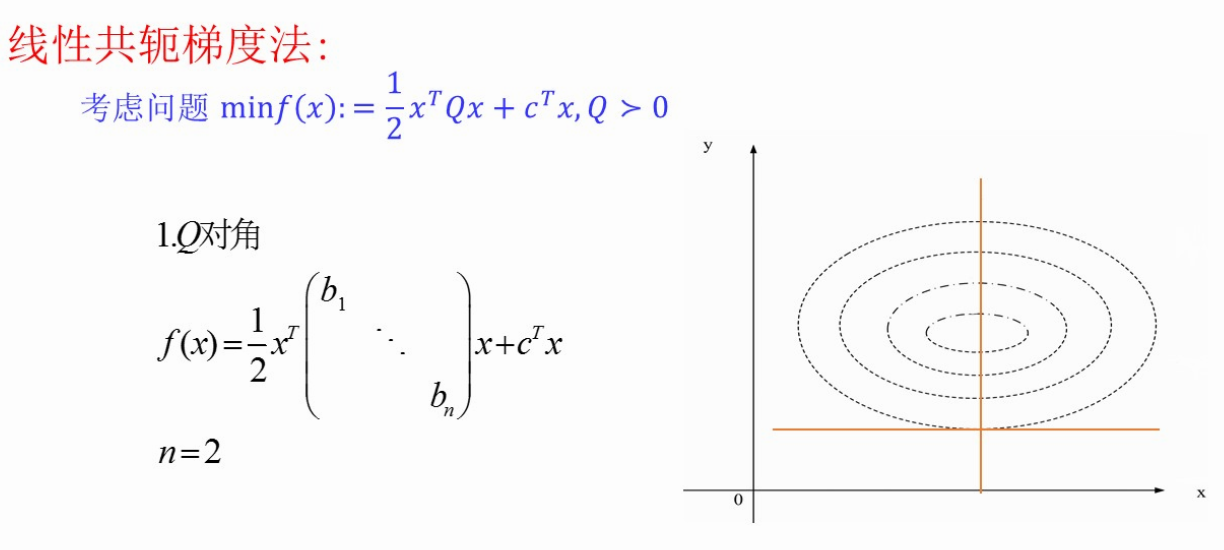
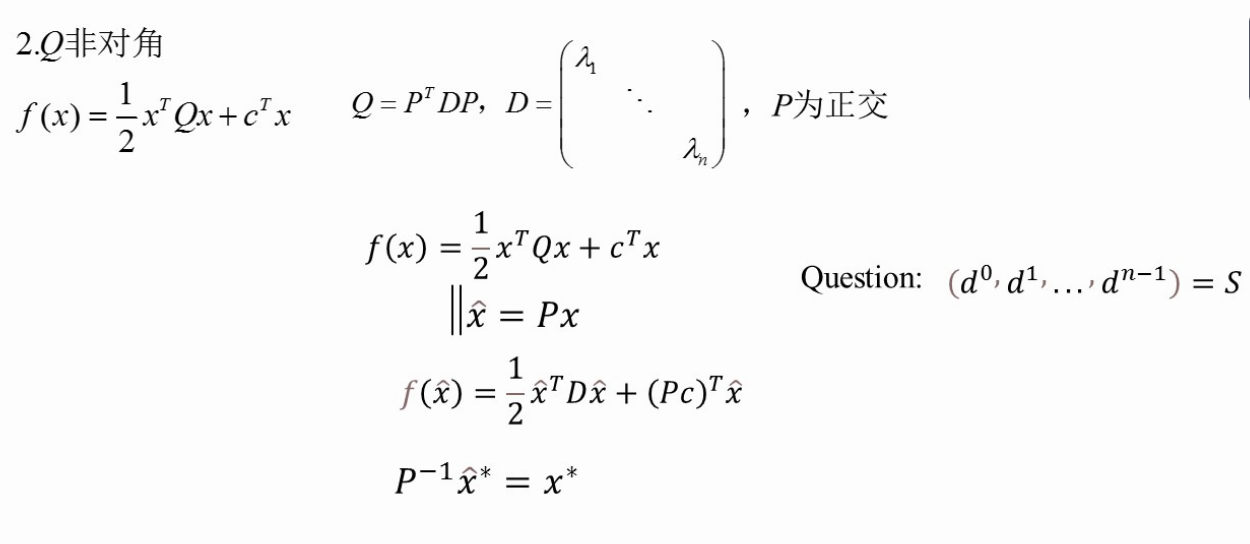
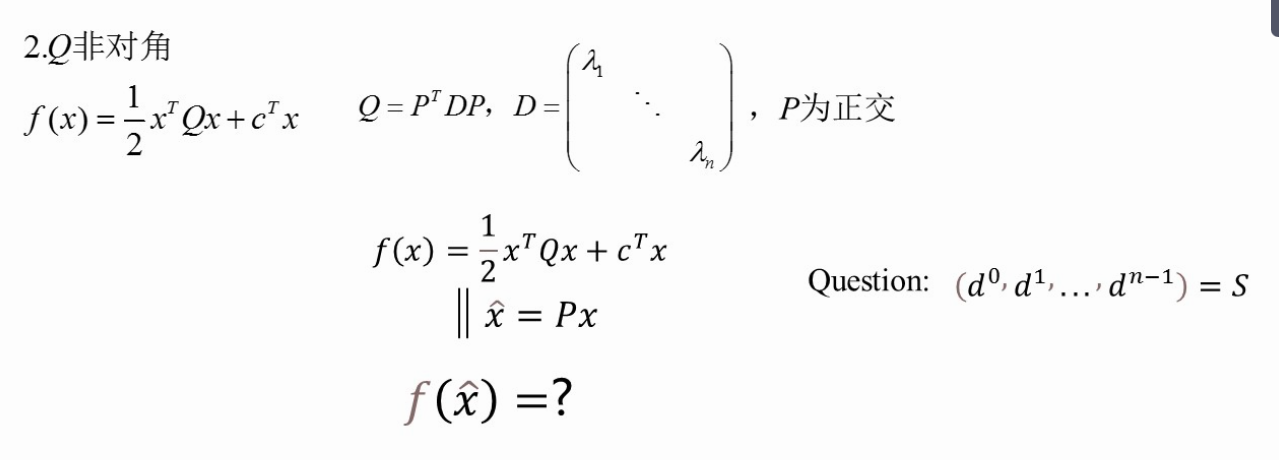


【习题】
(上图,求ak)

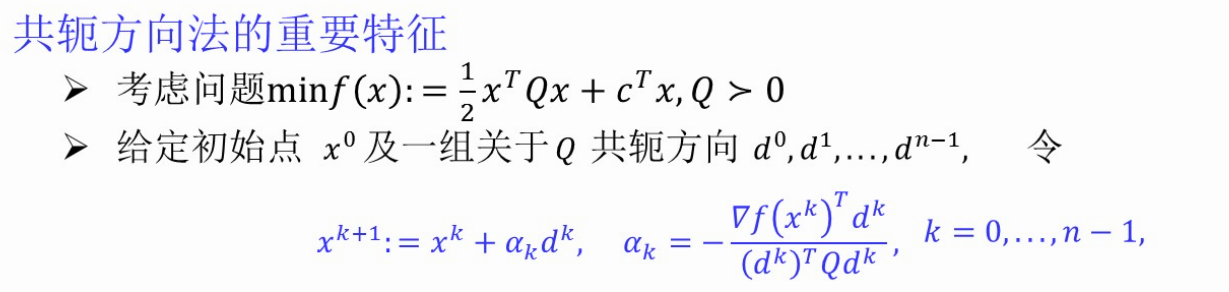


【描述共轭梯度法步骤★★★】
x_0, d_0=-▽f(x_0), ε>0, k=0
while(true) {
if () return
a_k = ...
x_k+1 = x_k + a_k*d_k
d_k+1 = ...
k = k+1
}

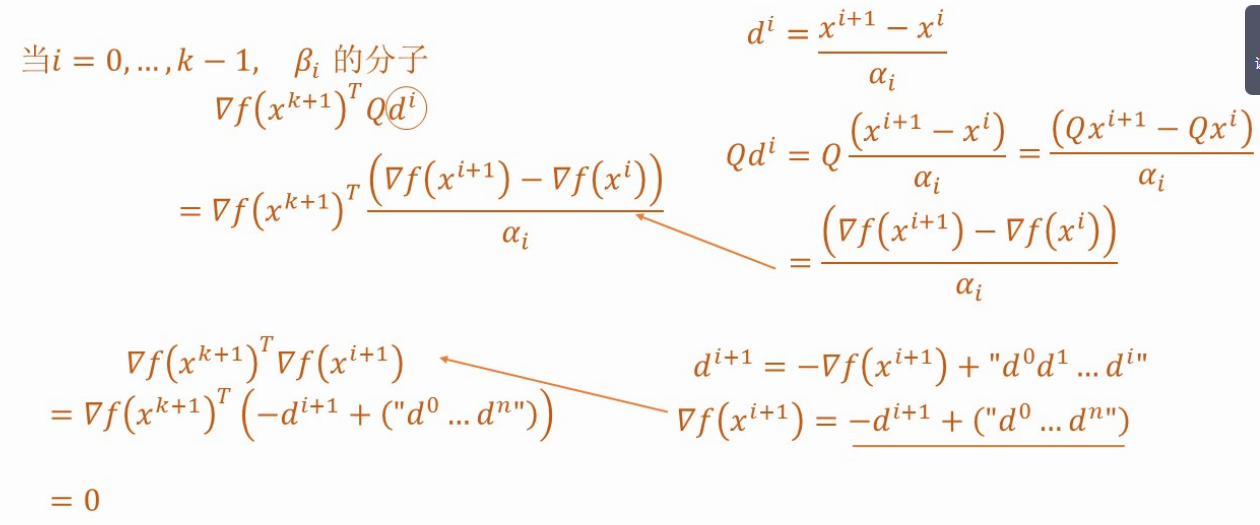
(三)约束最优化理论
1、+第8-9讲 KKT最优性条件
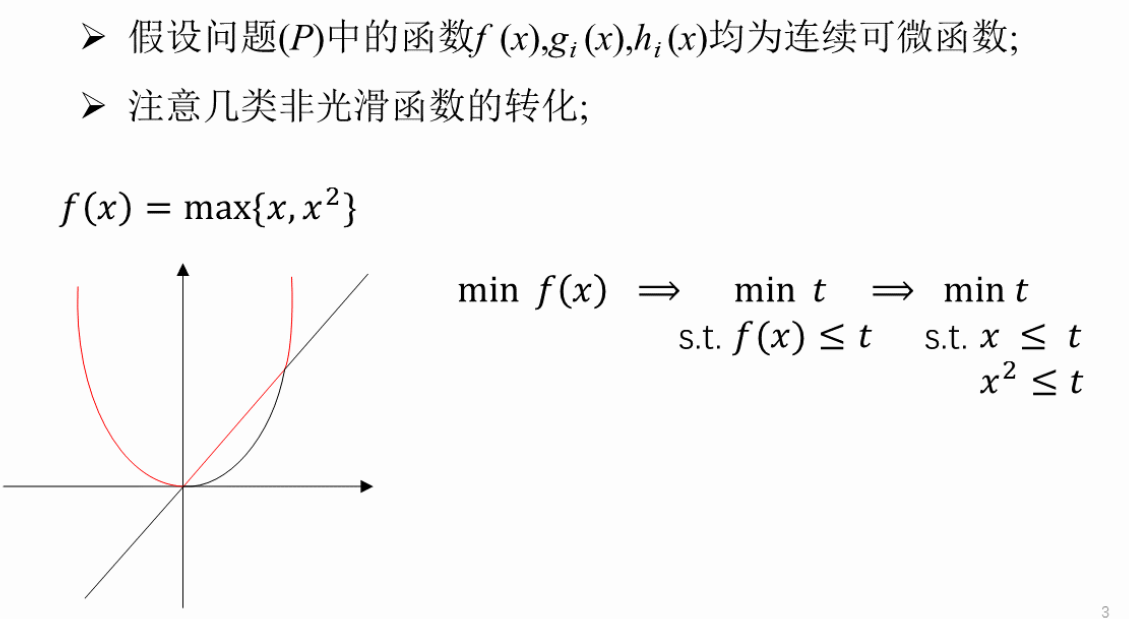
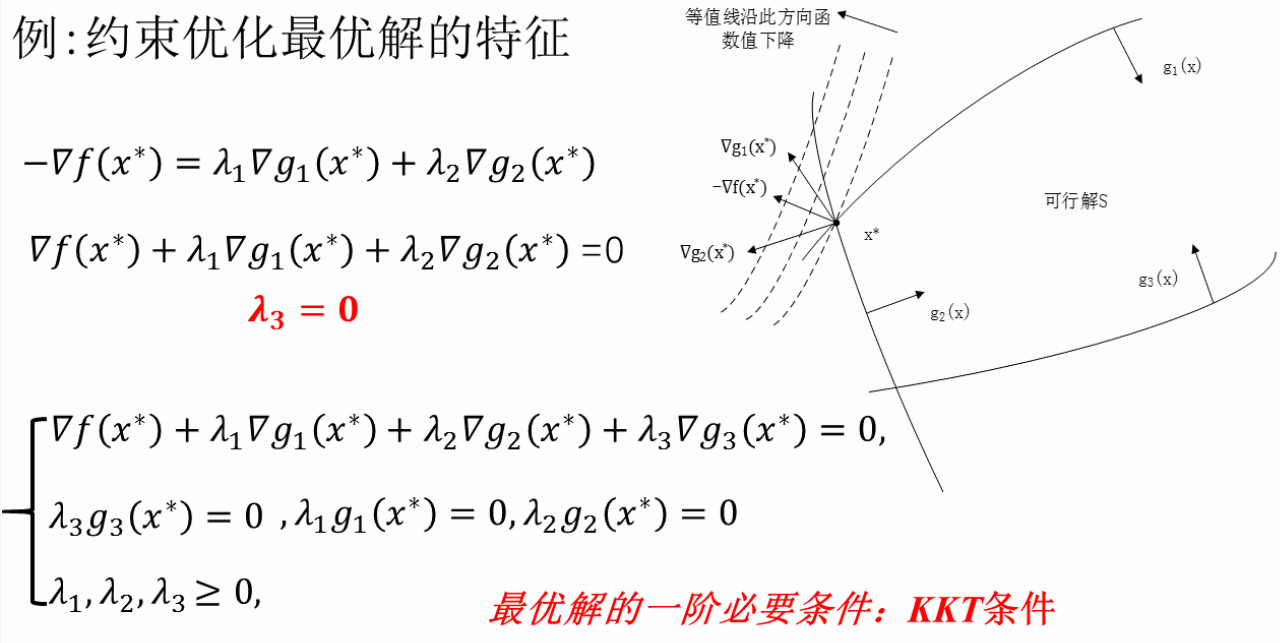






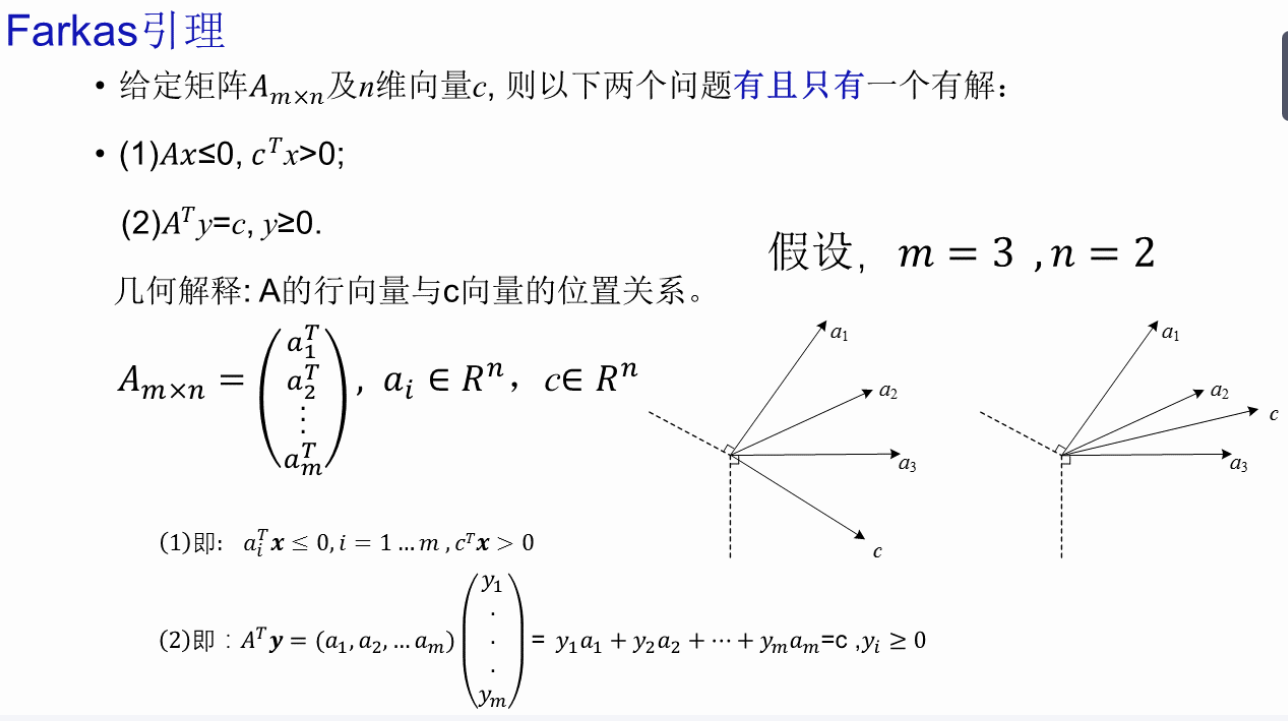

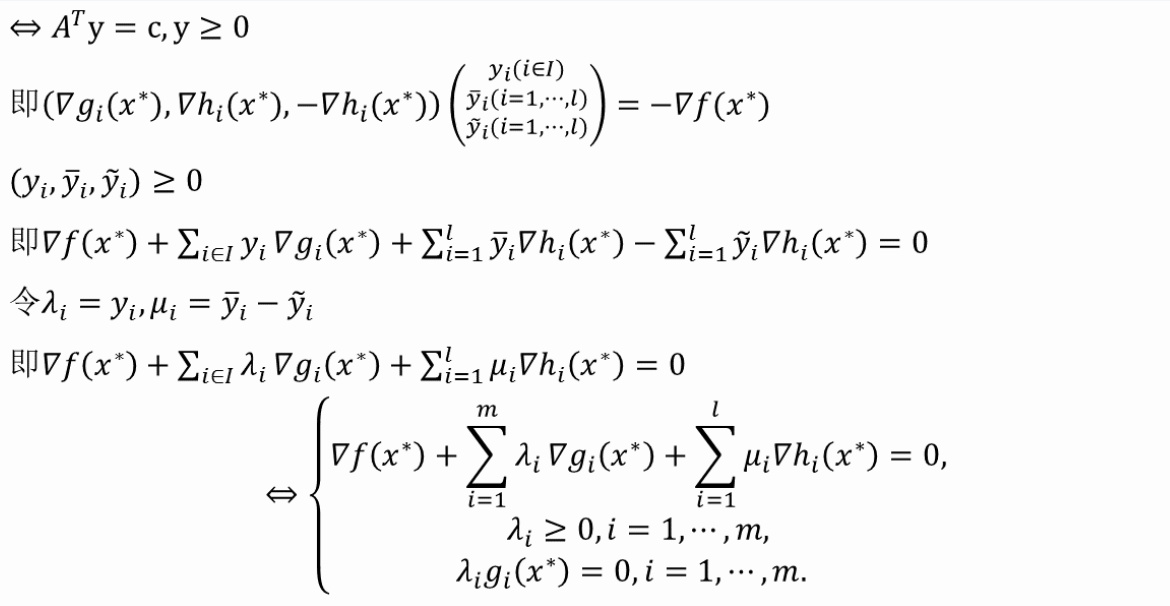



2、+第10讲 对偶理论









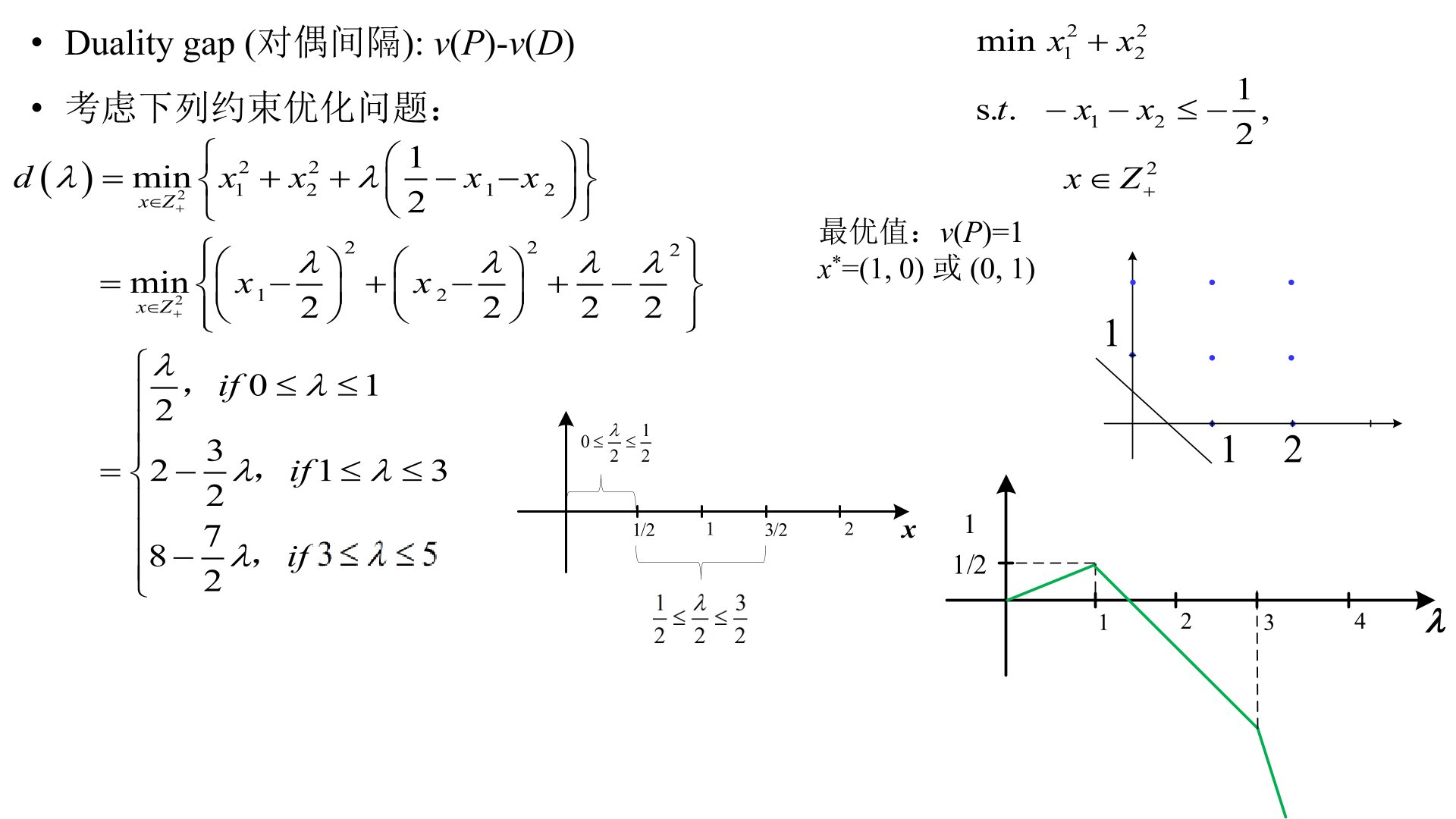



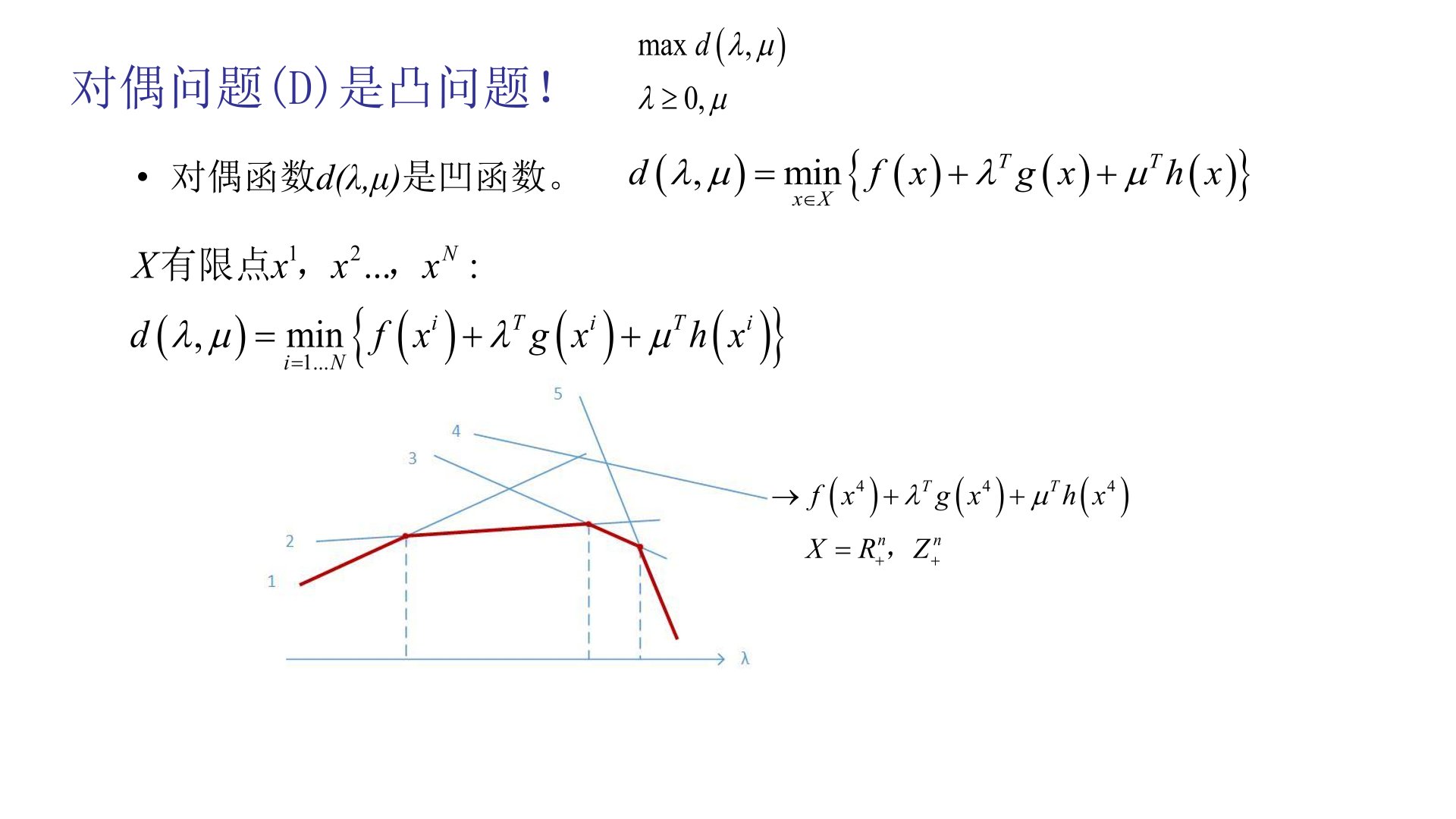

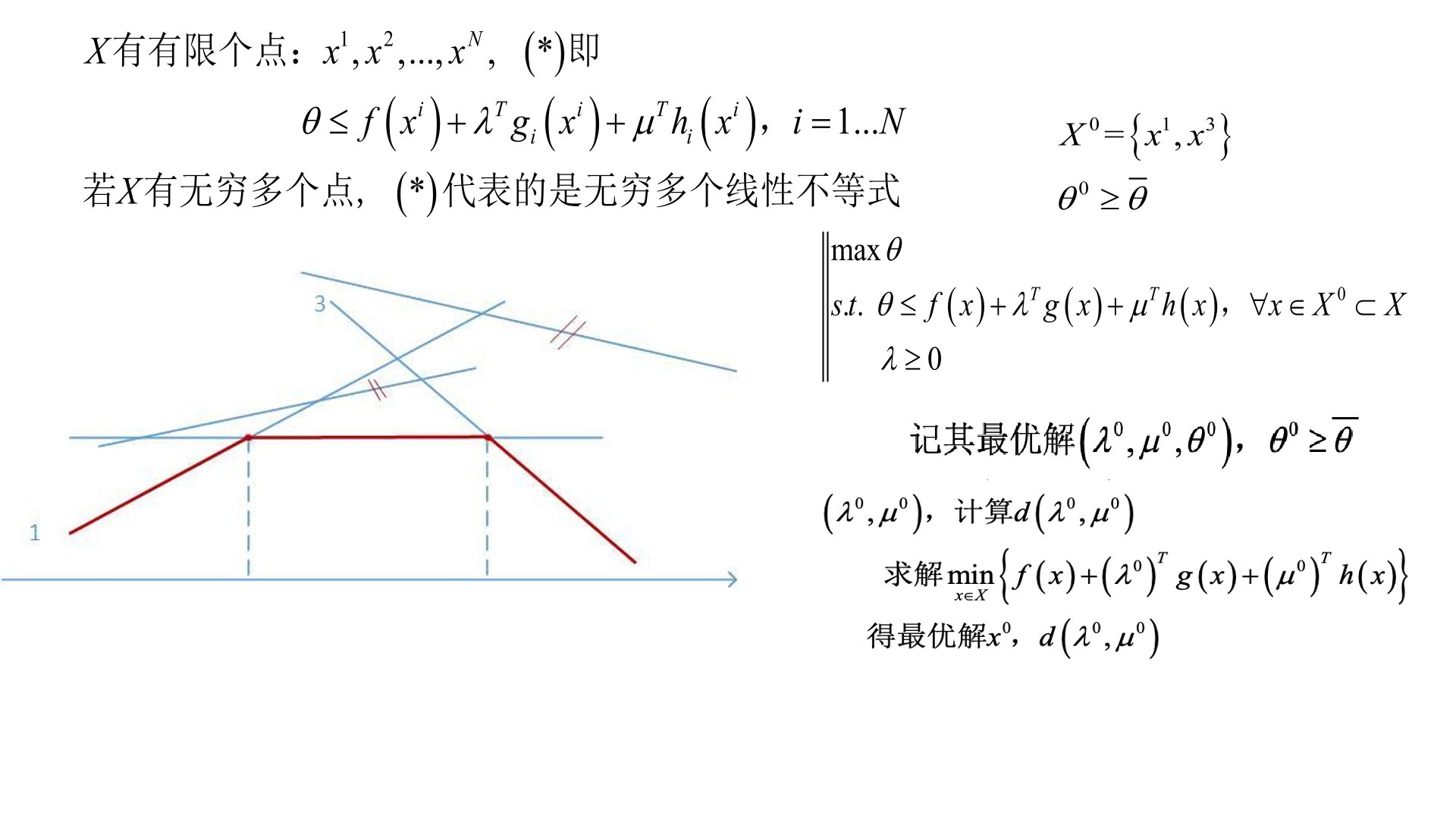
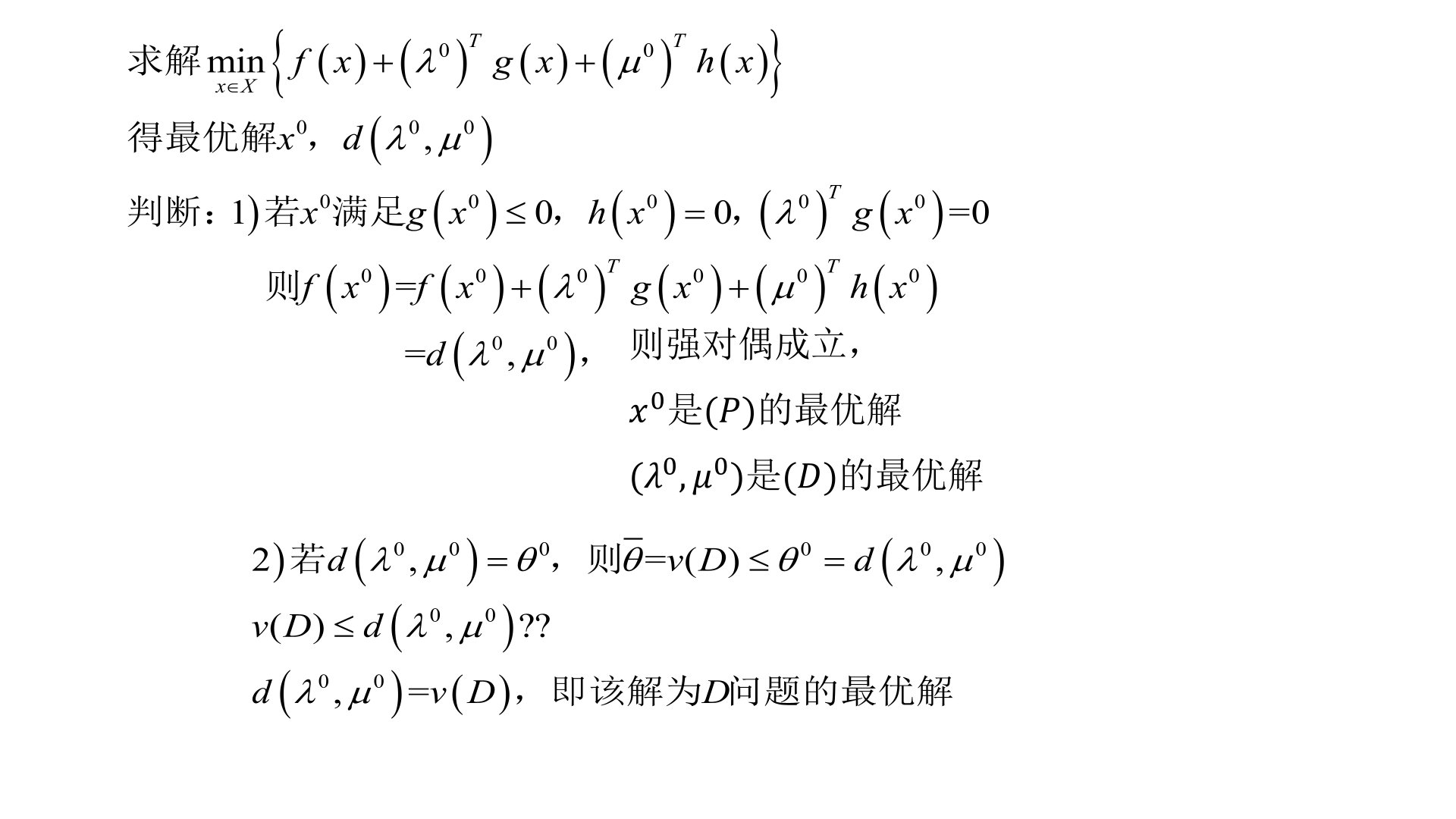



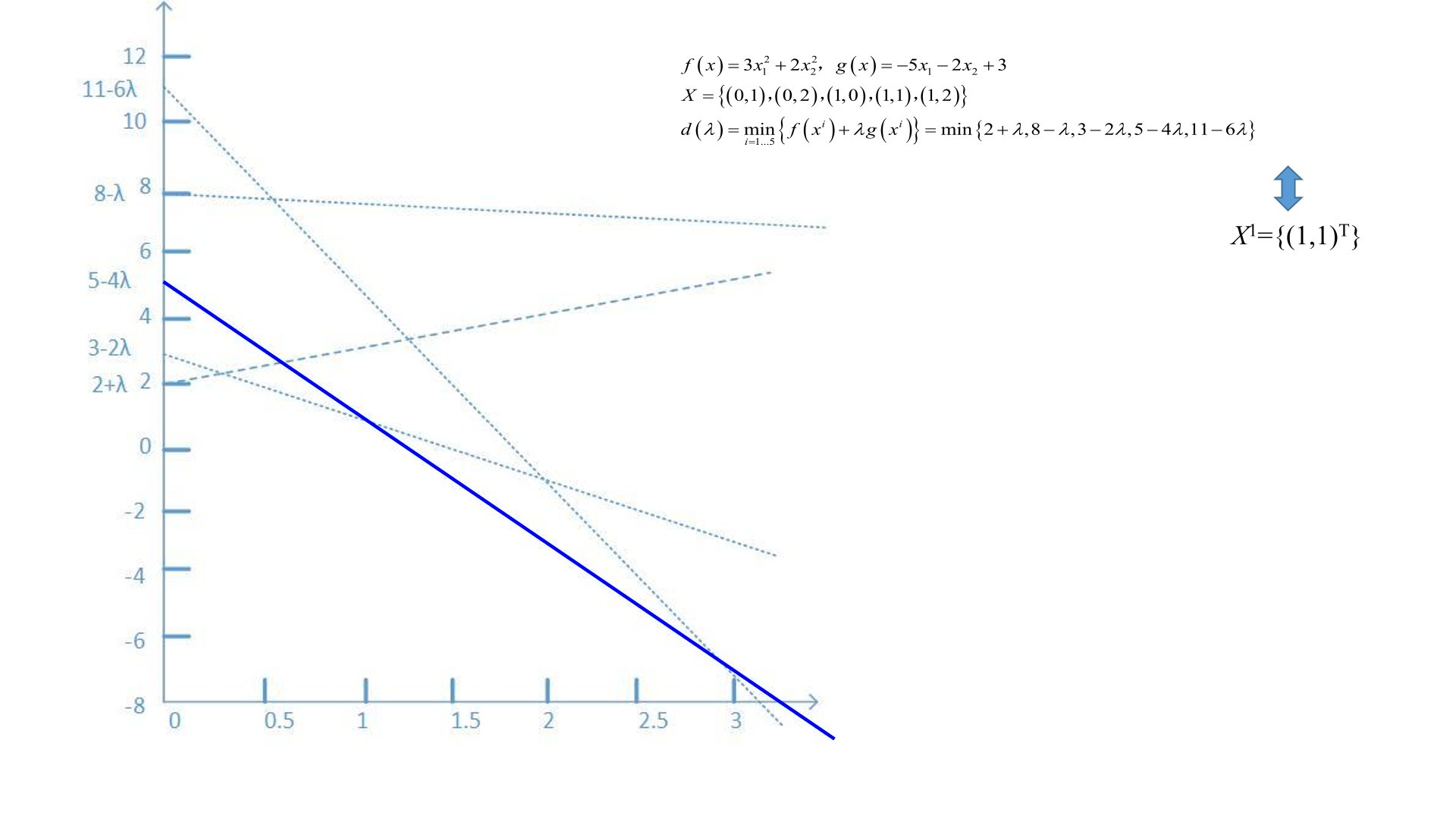
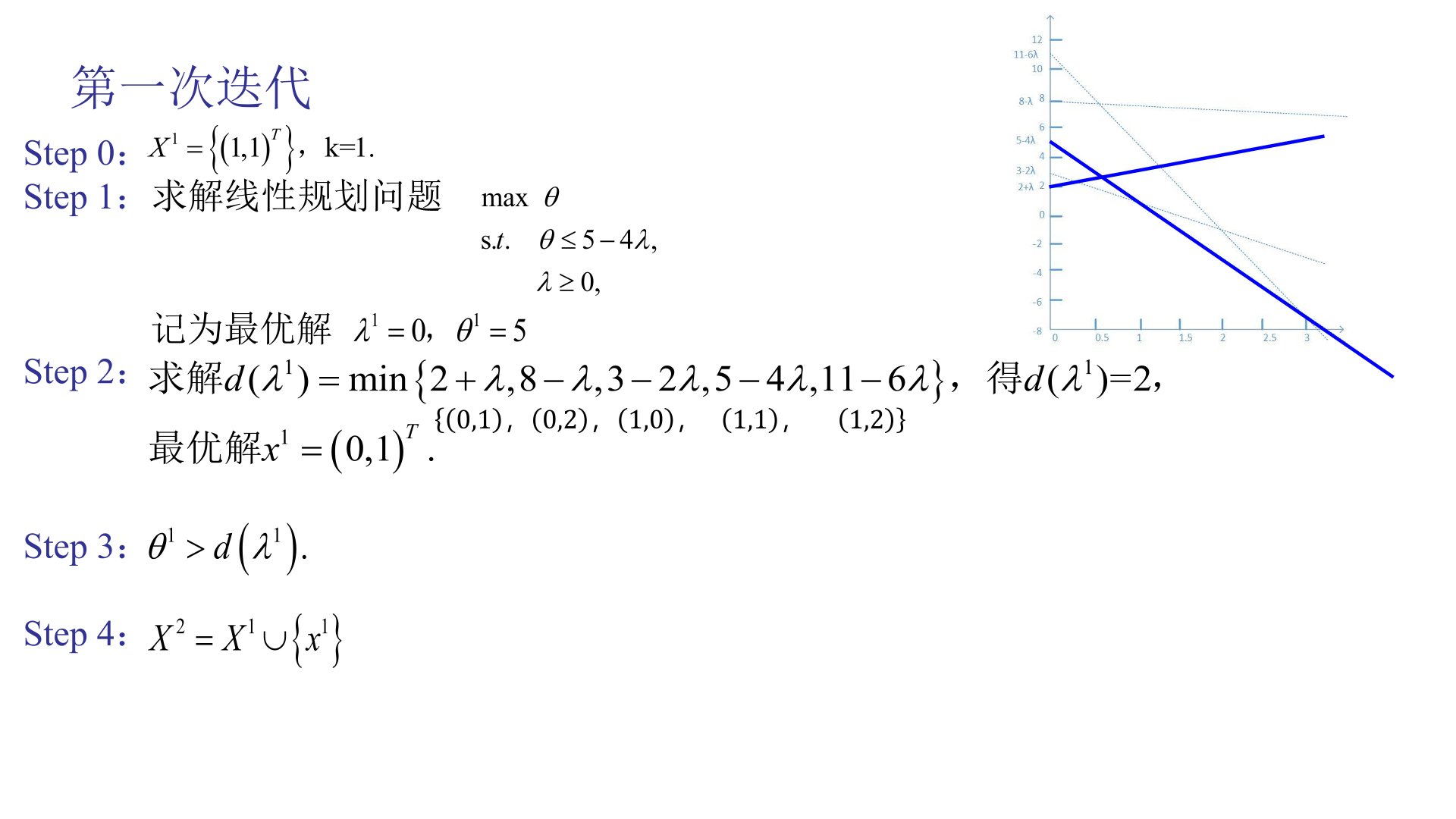
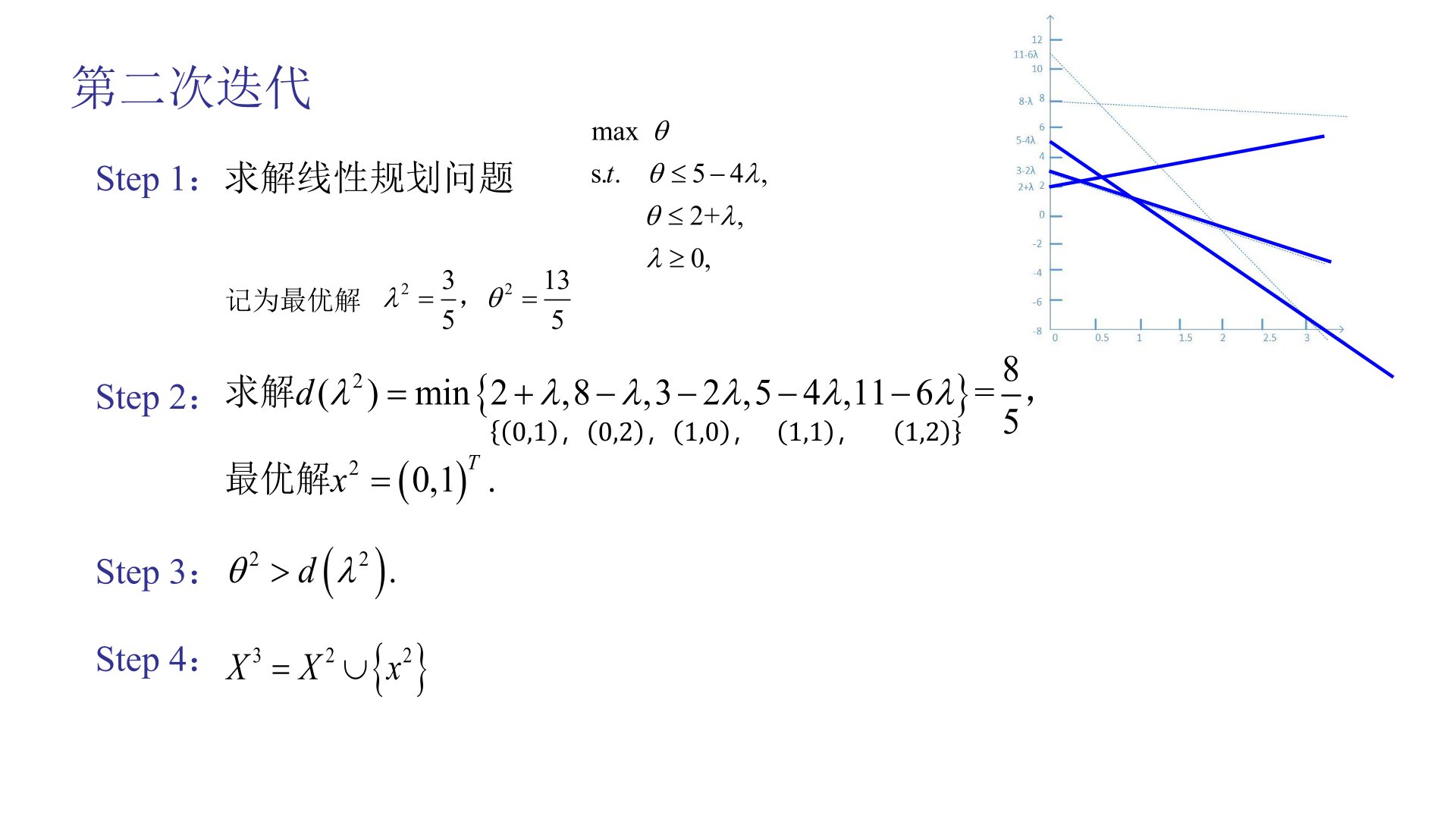

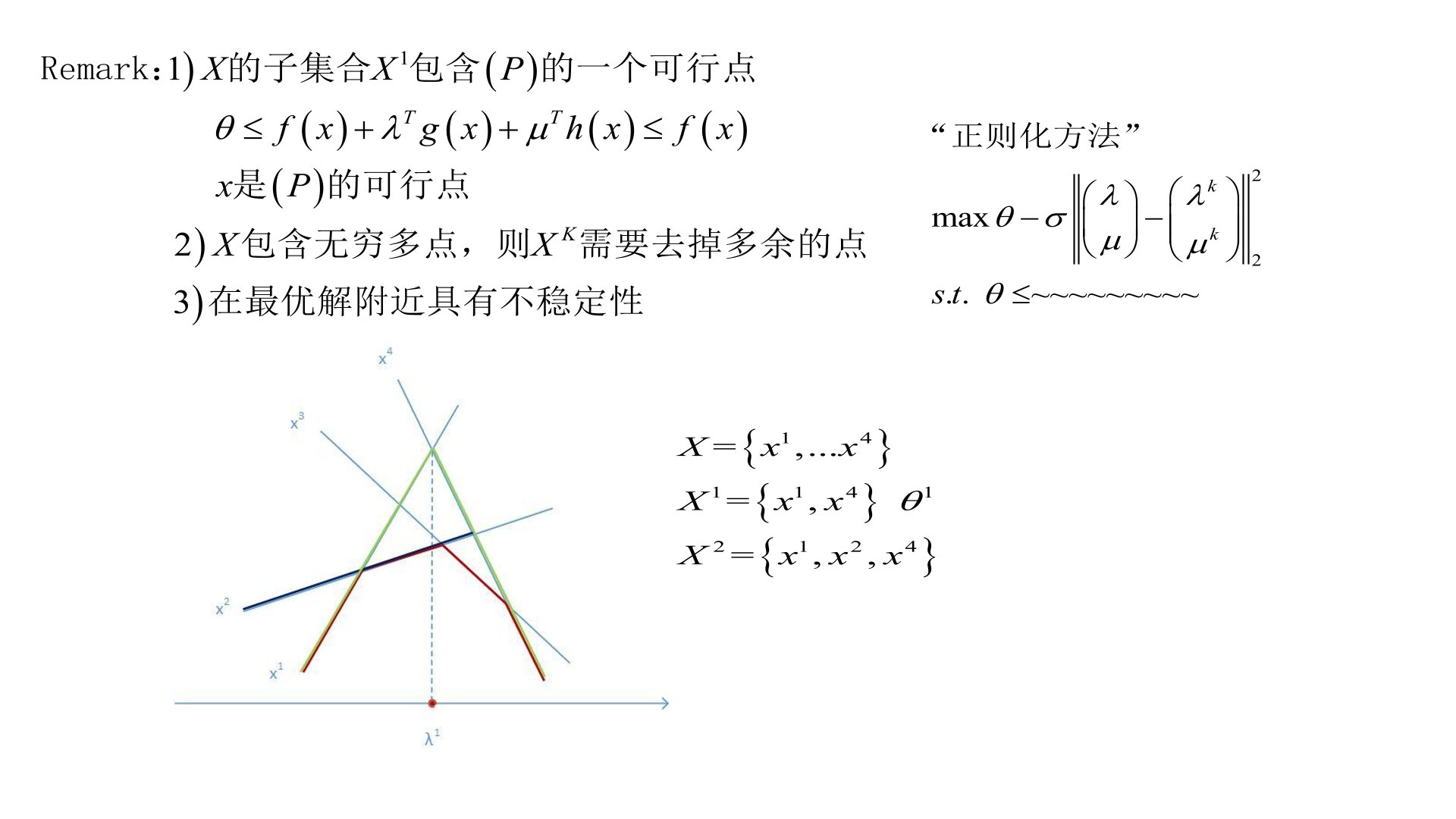
(四)拓展
第11讲 信息论
熵、信息熵、交叉熵、KL散度
熵是对随机变量 不确定性大小 的量化指标。不确定性越大,熵的值越高;确定性越高,熵的值越低。
信息熵就是上述的 “熵”,二者是同一个概念,“信息熵” 是全称,强调其在信息论中的含义 —— 表示编码一个随机变量的取值所需的平均比特数。
KL 散度又称相对熵,用于衡量 两个概率分布 P 和 Q 之间的相似程度。P 通常是真实分布,Q 是对 P 的近似分布。
交叉熵是 KL 散度的 “变形”,计算更简单,是分类任务中损失函数的核心(如逻辑回归、神经网络的交叉熵损失)。
本文系作者 @xiin 原创发布在To Future$站点。未经许可,禁止转载。



全部评论 1
anonymous
Google Chrome Windows 10