【数据结构与算法】二叉查找树的操作
《数据结构实验指导 - C++语言版》题目集 算法11-4~6 二叉查找树的操作
请编写程序,实现二叉查找树的插入、删除、查找操作,并完成简单的测试。
输入格式:
输入首先给出一个正整数 n(≤10),随后一行给出 n 个不重复的整数。最后一行给出一个测试用的整数 key。
输出格式:
执行以下操作并输出:
- 将给出的 n 个不重复的整数顺次插入一棵初始为空的二叉查找树。
- 查找 key 是否在树中。如果找到了,在一行中输出
Found key =key;否则输出NotFound.。 - 将 key 从树中删除。注意:如果要求从树中删除一个不存在的结点,应该在一行中输出错误信息
错误:x不在树中。,其中x是被要求删除的结点键值。 - 再次查找 key 是否在树中。如果找到了,在一行中输出
Found key =key;否则输出NotFound.。
输入样例 1:
8
4 3 6 8 7 1 2 5
5输出样例 1:
Found key = 5
NotFound.输入样例 2:
8
4 3 6 8 7 1 2 5
9输出样例 2:
NotFound.
错误:9不在树中。
NotFound.#include <bits/stdc++.h>
using namespace std;
struct Node {
int val;
Node* left;
Node* right;
Node(int x) : val(x), left(nullptr), right(nullptr) {}
};
struct Tree {
Node* root;
// 查找节点
bool find(int val) {
if (root == nullptr) {
cout << "NotFound." << '\n';
return false;
}
Node* cur = root;
while (cur != nullptr) {
if (cur->val == val) {
cout << "Found key = " << val << '\n';
return true;
} else if (cur->val < val) {
cur = cur->right;
} else {
cur = cur->left;
}
}
cout << "NotFound." << '\n';
return false;
}
// 插入节点
void insert(int val) {
if (root == nullptr) {
root = new Node(val);
return;
}
Node* pre = nullptr;
Node* cur = root;
while (cur != nullptr) {
pre = cur;
if (cur->val == val) {
return; // 跳过重复值
} else if (cur->val < val) {
cur = cur->right;
} else {
cur = cur->left;
}
}
cur = new Node(val);
pre->val < val ? pre->right = cur : pre->left = cur;
}
// 删除节点:核心修正根节点处理逻辑
bool del(int val) {
Node* pre = nullptr;
Node* cur = root;
// 步骤1:查找待删除节点 cur 及其父节点 pre
while (cur != nullptr && cur->val != val) {
pre = cur;
cur = cur->val < val ? cur->right : cur->left;
}
// 待删除节点不存在
if (cur == nullptr) {
cout << "错误:" << val << "不在树中。" << '\n';
return false;
}
// 步骤2:处理三种删除场景
if (cur->left == nullptr || cur->right == nullptr) {
// 场景1:叶子节点 或 只有一个子树(pre->left = child(可为null))
Node* child = cur->left ? cur->left : cur->right; // 子节点(可能为null)
// 【场景3】根节点删除时,直接更新 root 指针
if (cur == root) { // if (pre == nullptr) {
root = child; // 子树接替根节点(child为null则树为空)
} else {
// 普通节点:让子节点接替当前节点
pre->left == cur ? pre->left = child : pre->right = child;
}
delete cur; // 释放当前节点内存,避免泄漏
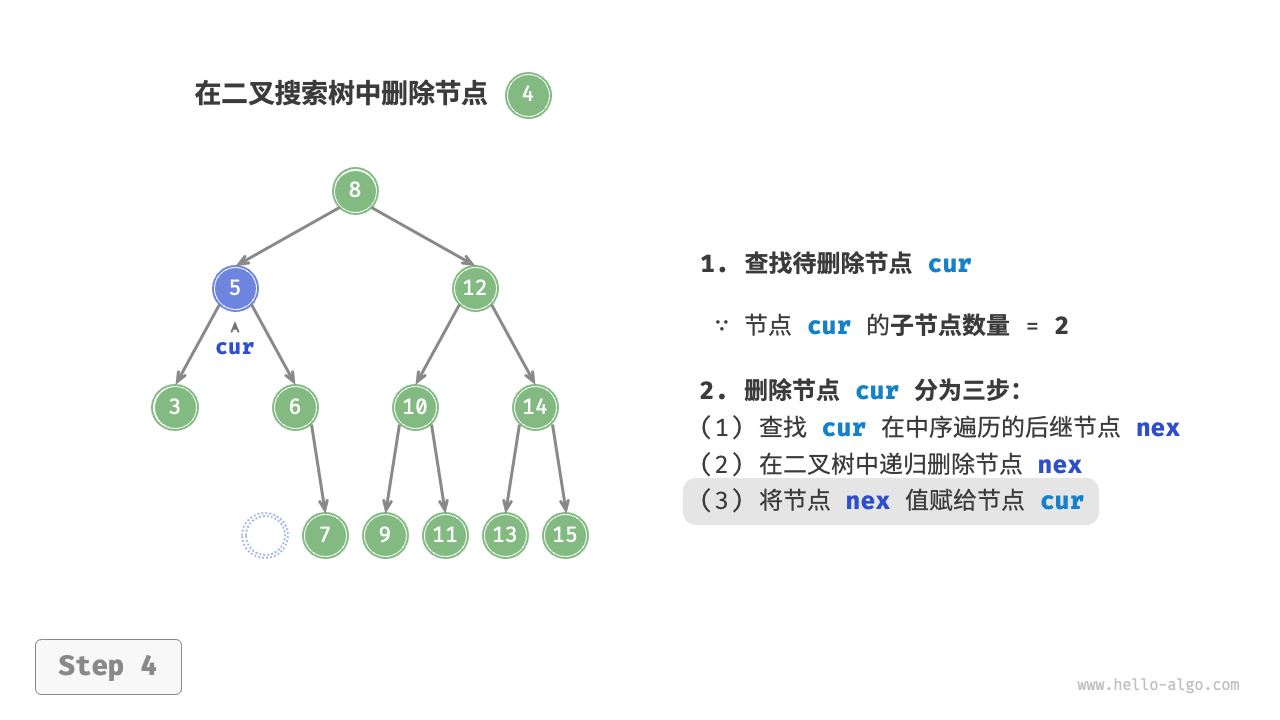
} else {
// 场景2:有两个子树,找后继节点(右子树最小节点)
// 我们无法直接删除它,而需要使用一个节点替换该节点。
// 由于要保持二叉搜索树“左子树 < 根节点 < 右子树”的性质,
// 因此这个节点可以是右子树的最小节点或左子树的最大节点。
Node* succ = cur->right;
while (succ->left != nullptr) { // 技巧,succ->left != nullptr找到最后一个非空节点
succ = succ->left; // 后继节点是右子树最左侧节点
}
// 递归删除后继节点(后继最多只有右子树,按场景1处理)
del(succ->val);
// 用后继节点的值覆盖当前节点(间接删除当前节点的值)
cur->val = succ->val;
}
return true;
}
// 构造函数:初始化根节点为空
Tree() : root(nullptr) {}
// 析构函数:递归释放整棵树内存,避免泄漏
~Tree() {
destroy(root);
}
private:
// 辅助函数:后序遍历释放所有节点内存
void destroy(Node* node) {
if (node == nullptr) return;
destroy(node->left); // 先释放左子树
destroy(node->right); // 再释放右子树
delete node; // 最后释放当前节点
}
};
int main() {
int n;
cin >> n;
vector<int> a(n);
Tree* t = new Tree(); // 动态创建Tree对象
// 插入节点
for (int i = 0; i < n; i++) {
cin >> a[i];
t->insert(a[i]);
}
// 查找并删除节点
int m;
cin >> m;
t->find(m);
t->del(m);
t->find(m);
// 释放Tree对象内存(触发析构函数,释放整棵树)
delete t;
return 0;
}
版权申明
本文系作者 @xiin 原创发布在To Future$站点。未经许可,禁止转载。



暂无评论数据