CSAPP：第2章 信息的表示和处理 2.3 整数运算

2.3 整数运算

1.无符号加法

• 无符号数加法

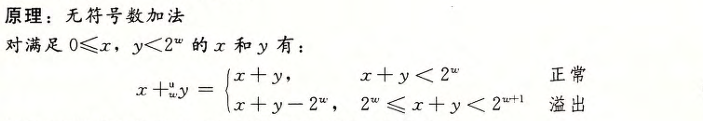
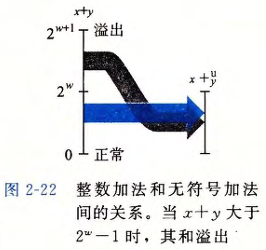
• 检测溢出

• 无符号数求反

在计算机中，无符号数的“求反”（模加法逆元） 指的是按位取反后+1★，而不是数学上的“相反数”（负数），因为无符号数没有符号位，不能直接表示负数。

2.补码加法

• 补码加法

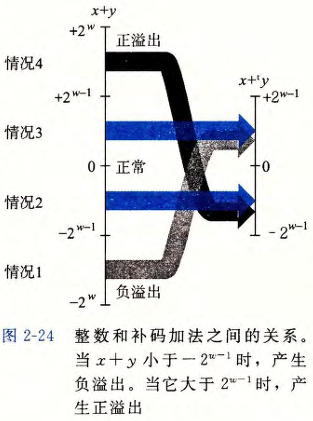
• 溢出检测★

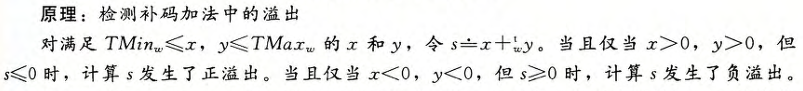
3.补码的非

• 补码的非 = 按位取反 + 1

（这里的 “(-x)” 在补码语境下，就是通过 “按位取反 + 1” 得到的补码非）

• 为什么TMin取反还是本身？

对 8 位 TMin（1000 0000）执行「按位取反 + 1」：

1. 按位取反：把每一位 0 变 1、1 变 0 → 0111 1111（对应十进制 127）；
2. 加 1：0111 1111 + 1 = 1000 0000（二进制）→ 又回到了 TMin 的补码 1000 0000（对应十进制 - 128）。

• 计算一个数x的补码非的第二种方法

此方法是建立在将位向量分为两部分的基础之上的。假设 k 是最右边的 1 的位置，我们对位 K 左边的所有位取反即可。

「找最右 1 的位置 k，取反 k 左侧所有位」的本质，是利用了：

1. 最右 1 的右侧全是 0，按位取反后全是 1，加 1 会让这部分全回 0，且仅向 k 位进 1；
2. k 位的 1 取反后是 0，加进位 1 又变回 1，相当于 k 位 “没变”；
3. 只有 k 左侧的位，在按位取反后没有被进位影响，最终仅保留 “左侧取反” 的结果。

这个方法是对「按位取反 + 1」的优化 —— 不用先全取反再加 1，只需定位最右 1，仅处理左侧位，底层硬件（比如 CPU 的neg指令）甚至会用这个逻辑来加速补码非的计算。

4.无符号乘法

5.补码乘法

C语言中的有符号乘法是通过将2w位的乘积截断为w位来实现的。将一个补码数截断为w位相当于先计算该值模2^w，再把无符号数转换为补码。

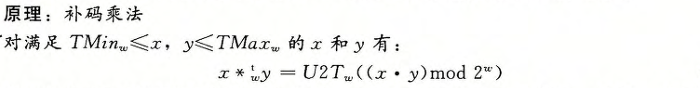
6.乘以常数

• 乘以2的幂

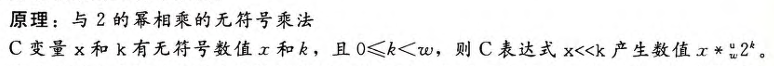
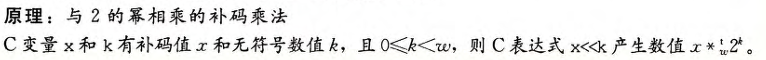
7.除以2的幂

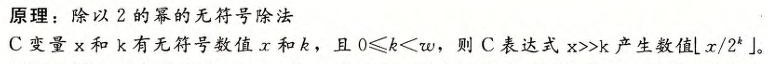
在 C 语言中，整数除法的 “向下舍入” 并非数学意义上的向下取整，而是严格的 “向零舍入（Truncation towards zero）”。

有符号整数，且可能为负，直接右移相当于除以2^k向下取整，导致-7/4=-2，并非想要的向0舍入，因此编译器会对除法底层算法（该数除以2的n次幂）进行修正。（我们可以通过在移位之前“偏置(biasing)”这个值，来修正这种不合适的舍入。）

int divide(int x) {
    return x / 4;  // 不能简单右移！
}

-7 / 4 = floor((-7+3)/4) = floor(-4/4) = -1

8.关于整数运算的最后思考

计算机执行的“整数”运算实际上是一种模运算形式。