LeetCode 98. 验证二叉搜索树 [Hot 100]

98. 验证二叉搜索树

已解答

中等

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 严格小于 当前节点的数。
• 节点的右子树只包含 严格大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

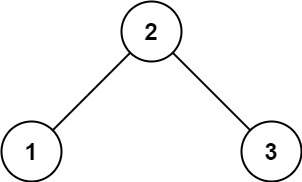
输入：root = [2,1,3]
输出：true

示例 2：

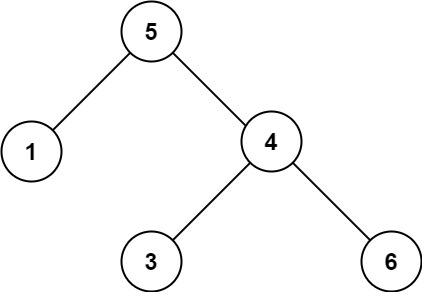
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

方法一（范围验证）

• 使用long类型来避免整数边界值问题
• 递归检查每个节点是否在允许的范围内
• 左子树的上限是当前节点值，右子树的下限是当前节点值

/**
 * Definition for a binary tree node.
 */
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public boolean isValidBST(TreeNode root) {
        return validate(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }
    
    private boolean validate(TreeNode node, long min, long max) {
        if (node == null) {
            return true;
        }
        
        // 检查当前节点值是否在允许范围内
        if (node.val <= min || node.val >= max) {
            return false;
        }
        
        // 递归检查左子树和右子树
        // 左子树的所有节点值必须小于当前节点值，所以上限是当前节点值
        // 右子树的所有节点值必须大于当前节点值，所以下限是当前节点值
        return validate(node.left, min, node.val) && validate(node.right, node.val, max);
    }
}

方法二（使用Integer对象避免边界问题）

• 使用Integer对象可以避免边界值问题，通过null表示无穷大/无穷小
• 逻辑更清晰，避免了数据类型边界问题

推荐使用方法二，因为它避免了数据类型边界问题，代码更清晰易懂。

class Solution {
    public boolean isValidBST(TreeNode root) {
        return validate(root, null, null);
    }
    
    private boolean validate(TreeNode node, Integer min, Integer max) {
        if (node == null) {
            return true;
        }
        
        // 检查当前节点值是否在允许范围内
        if ((min != null && node.val <= min) || (max != null && node.val >= max)) {
            return false;
        }
        
        // 递归检查左子树和右子树
        return validate(node.left, min, node.val) && validate(node.right, node.val, max);
    }
}

方法三（利用BST中序遍历有序的特性）

• 利用BST中序遍历结果是有序数组的特性
• 在中序遍历过程中检查当前节点是否大于前一个节点
• 如果遍历过程中发现违反有序性，则不是有效的BST

class Solution {
    private Integer prev = null;
    
    public boolean isValidBST(TreeNode root) {
        return inorderTraversal(root);
    }
    
    private boolean inorderTraversal(TreeNode node) {
        if (node == null) {
            return true;
        }
        
        // 遍历左子树
        if (!inorderTraversal(node.left)) {
            return false;
        }
        
        // 检查当前节点是否大于前一个节点
        if (prev != null && node.val <= prev) {
            return false;
        }
        prev = node.val;
        
        // 遍历右子树
        return inorderTraversal(node.right);
    }
}

中序遍历的工作原理

中序遍历的顺序是：左子树 → 当前节点 → 右子树

对于BST来说，中序遍历的结果应该是一个严格递增的序列。

为什么能够判断"后节点大于中间节点"？

让我们通过一个具体的遍历过程来看：

// 二叉树示例：
//     5
//    / \
//   3   7
//  / \   \
// 1   4   9

// 中序遍历结果：1 → 3 → 4 → 5 → 7 → 9

遍历过程：

1. 遍历到节点1（第一个节点，prev = null，直接通过）
2. 遍历到节点3：检查 3 > 1 ✓，prev = 3
3. 遍历到节点4：检查 4 > 3 ✓，prev = 4
4. 遍历到节点5：检查 5 > 4 ✓，prev = 5
5. 遍历到节点7：检查 7 > 5 ✓，prev = 7
6. 遍历到节点9：检查 9 > 7 ✓

关键理解：递归的"栈帧"机制

中序遍历是深度优先的，递归调用会维护一个调用栈：

// 遍历到节点5时的调用栈：
inorder(5)
  → inorder(3)        // 左子树
    → inorder(1)      // 左子树的左子树
    ← 返回，prev=1
    → 检查3>1 ✓，prev=3
    → inorder(4)      // 左子树的右子树
      → 检查4>3 ✓，prev=4
    ← 返回
  ← 返回，prev=4
  → 检查5>4 ✓，prev=5  // ★ 这里确保了5大于左子树的最大值4
  → inorder(7)        // 右子树